Nonlinear Structural Analysis

In simplest terms a Nonlinear structural analysis is one that considers other secondary effects that may have an impact on the structure's response to the loads applied. In comparison, a Linear Structural Analysis does not consider the possibility of any secondary effects. The most well-known nonlinear structural effect is P- Delta; vertical loads on a leaning pole causing additional bending moments.

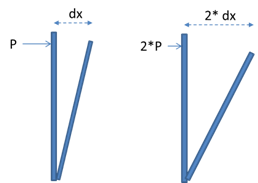Understanding linear structural analysis will facilitate a better understanding of the Nonlinear method. There are several methodologies that fall into the linear category, but they all have one thing in common. In a linear structural analysis, the structure is assumed to be perfectly elastic and totally linear in its response to forces.

This means that if a given force was applied to a portion of a structure and it deflects a specific amount; doubling the force should generate twice the amount of deflection. This enables, for linear analysis, the principle of superposition of forces. You could analyze the response of the structure to each force individually and add up (superimpose) all of the calculated deflections (or stresses) to arrive at a final response for the structure. The simplicity of this method is very attractive.

The linear methodology assumes many factors which may or may not be accurate. For this reason the linear methodology has required higher load and safety factors by some National codes in the past to account for these assumptions. In Nonlinear methodology, the primary assumptions used in the linear methodology are considered and addressed. The end result is a much more accurate estimation of the structure's response (deflection, stress, etc.).

With the use of linear methodology, the possibility of the structure becoming unstable had to be evaluated separately from the loading analysis. It is conceivable that a specific linear analysis could show that the structure's components are well below yield point stresses, yet the total structure could be in a failure state. For example, to estimate the stability of a single pole structure to resist vertical loads, Euler's buckling formula was modified by Gere and Carter to take a single pole's taper into account. This in itself is still just an estimate with its own set of assumptions factored in. The principle assumption is that no attachments offer any stability to the pole along its length. Structures consisting of more than one element (i.e. most Transmission Structures) are very difficult to analyze using linear methodologies.

In Nonlinear Structural Analysis, the stability of the structure is determined as part of the complete solution procedure. Structures that are not stable simply do not converge on a final solution or the determined deflections are that of a collapsed structure.

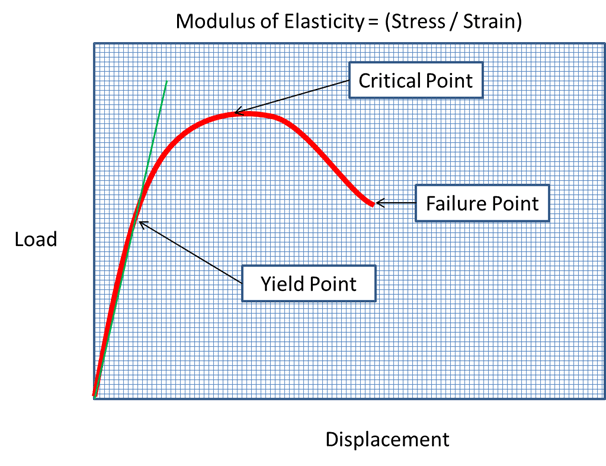As loads are initially applied in small amounts to a structure, the structure will respond in an approximately linear manner. At some point, other (secondary) effects begin to influence how the structure responds. This occurs at a point that can be referred to as the Yield Point for the structure, which is similar to the Yield Point of most metals. As the loads are increased on the structure, these secondary effects will become very significant and the structure is said to 'soften' or become less stiff. Once the loads reach what is called a Critical Point, the structure will no longer be able to resist the loads. The result is rapid displacement of the structure components towards the Failure Point where the ultimate failure of the structure and its materials occurs rapidly. In other words the structure collapses or buckles.

The following sections are all the possible secondary effects that are commonly associated with the term "Nonlinear Structural Analysis" with commentary on how applicable they are to Transmission and Distribution Line Structures.