Nonlinear Structural Analysis

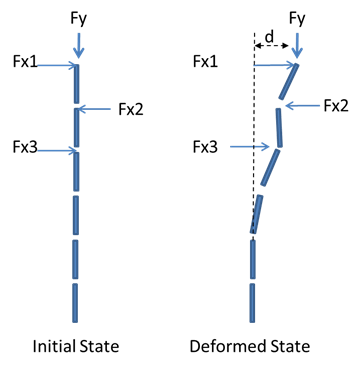As a structure deforms/deflects in response to the loads applied to it, the fact that the loads are essentially moved to a different absolute location will change the real loads being applied to the structure. The magnitude and direction of the structure's deflection at loading points will in itself introduce additional loads for the structure to deal with.

For any structure that is expected to stay stable and fixed in one place (all Transmission and Distribution structures), the equations of equilibrium apply to all forces and moments at every point along the structure. So if a vertical force is displaced horizontally, the structure must resist with the appropriate amount of counter-balancing forces and moments in order to completely compensate for this effect. The example shown above in the deformed state is what is commonly called the P-delta effect where the force (P or Fy) times the distance (delta or d) represents the high-level estimation of the bending moments that the structure must resist, over and above the initial loads.

The two-dimensional example above hints at some of the details of this calculation. Of course real structures are three-dimensional and they are exposed to other forces in different directions that are displaced in directions that also create additional moments. Although a single-pole structure is depicted above, these same effects exist in multi-pole, truss and other structure types as well.

Another Geometric Nonlinearity occurs to structure members, including downguys, since their three dimensional stiffness factors change with structure deflection.

It is almost a certainty that all structures will be modeled using Finite Element techniques as part of any Nonlinear analysis. This is a technique whereby the structure is modeled into many discrete elements which are then combined (based on the structure's geometry) into a larger model for the entire structure. The objective is to create a model that can satisfactorily "estimate" the overall structure's response. Its strength is the ability to model even very complex structures using simple, well understood elements. Generally, the more elements provided in the model, the more accurate will be the result.

The discrete elements are individually modeled (in matrix form) for how they respond to forces in three dimensions.

[F] = [k][d]
F = forces
k = element stiffness
d = local displacements

If an element's properties change with length (e.g. diameter of a pole) or its length is significant, best practices would suggest that an element be broken up into additional smaller elements. This will help provide a better estimate in element and structure responses.

In order to model an entire structure with a collection of element models, they are combined into a much larger model in a way that ensures the structure is statically determinant at every element boundary (sum of the forces and moments are zero). Applying the assumed loads at the element boundaries to the larger structure model will allow the calculation of global structure displacements, which in turn can be used to determine local element displacements and reactions (forces, moments, stresses). At this point you will have the calculation result based on a Linear Analysis. The models used assume a linear elastic response within each element and do not yet have any secondary effects included. It is however a necessary first step to get this initial estimate of structure and element responses.

The Geometric Nonlinear effects (such as p-delta) can now be estimated with known forces and displacements and then combined with the assumed loads into the structure model and calculated once more. This provides the first estimate of how the structure will respond to both the assumed loads and these secondary effects. The structure may now have deflected further or in different ways than initially estimated. The secondary effects should be re-calculated and re-applied to the structure model at least once more. This process continues until the deflections of the structure do not materially change, or it is obvious that the structure is unstable. If the applied loads are very close to, but not past, the Critical Point, it will take many iterations to reach a solution. If the structure is already past the Critical Point, these iterations will not converge on a solution.

All Nonlinear solutions must be solved iteratively as there is no way to combine Geometric Nonlinear effects into the structure or element models to solve in one calculation. Other secondary effects can be combined at each iteration step of the solution procedure discussed here, for efficiency. Given the large amount of matrix manipulation and the iterative procedure required, computer software tools are commonly used.