Quick Pole Knowledge Topics
- AccuracyReliable and precise
- Sags & Tensionof Span Attachments
- Nonlinear AnalysisWhat is it?
- Wood Pole Data used in Quick Pole
- Due DiligenceDiscussion
- Quick Pole ValidationCertification
- How Accurate are your Results?
- About Calculation Areas
- Nonlinear Sags & Tensions
- Linear Structure Response
- Nonlinear Structure Response
- Foundation Response
How Accurate are your Results?
The process of designing new pole lines or assessing existing lines for potential new attachments can be complex and the software used for Pole Line Design may assist with few or many parts of this process. At Sonideft we understand the complexities involved in the Pole Line Design Process and the many aspects that must be calculated and considered. We also understand the need to share knowledge on how Quick Pole calculates certain aspects so that users can better understand and become comfortable with the results and the concepts involved. Towards this end we will always expose many initial, interim and final results so that we can do our own quality control and to help walk users through the entire calculation process. For Professional Engineers as users, approvers or managers, we understand the need for their Due Diligence in understanding what the software will do for you, how it will do it and how well.
The focus of this article is on the "How well" question. Before we answer this question it is important to understand the major calculation areas and how they impact each other.
About Calculation Areas
Pole lines consist of two major components: Span Attachments (Wires, Cables...) and the Structures that support them. Many of the calculations can be complicated to compute and need be evaluated under multiple conditions and situations; which will be described in this section. These can be organized into the following main categories:
- Sags, Tensions and Clearances: What loads will the wire attachments exert on the structures that support them and what sags will they have? How much clearance will there be at certain points under the line? Have the nonlinear characteristics of the material in the wire been taken into account?
- Linear Structure Response: How does the structural analysis calculation process perform with guyed and unguyed structures under different scenarios and using different structure materials? This is a Linear Analysis based on Finite Elements.
- NonLinear Structure Response: How well are the Nonlinear Analysis methodologies applied to arrive on a consistent and accurate answer; considering the following:
- Nonlinearity of member reactions due to structure deflection (Geometric Nonlinearity)
- Nonlinearity of loads due to structure deflection (Load Nonlinearity).
- Is the structure stable under these conditions?
- Foundation: Can the structure's foundation withstand the necessary loads to support the structure?
The category order has been set in this way for a very important reason. The tension of span/wire attachments is the most significant load applied to structures. What you first need to understand is that calculating this value incorrectly or inaccurately will make all other calculations inaccurate as well. Even if all other calculation abilities were World Class in the software tool, Garbage In=Garbage Out.
 The propagation of error due to errors in the input loads from wire attachments (tensions) will propagate through all the other calculation categories. For instance, if a tension is calculated that is 20% off from the true results, you can expect that the other results could be off by a similar amount as well; even if the later categories do a perfect calculation. In some cases the error propagates in a linear fashion to the output of the next stage and in other cases it can cause a magnified effect. Regardless of the error transfer function, positive error differences by themselves will always propagate to positive errors in the final Analysis.
The propagation of error due to errors in the input loads from wire attachments (tensions) will propagate through all the other calculation categories. For instance, if a tension is calculated that is 20% off from the true results, you can expect that the other results could be off by a similar amount as well; even if the later categories do a perfect calculation. In some cases the error propagates in a linear fashion to the output of the next stage and in other cases it can cause a magnified effect. Regardless of the error transfer function, positive error differences by themselves will always propagate to positive errors in the final Analysis.
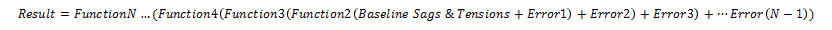
While the diagram may suggest that inaccuracies create higher values in the results, they can also be negative. At any stage of the analysis, the net result is the accumulation of values including the inaccuracies of the previous categories and from different items in the same category. An example would be calculating the tension of a #2 AWG Copper wire too low while also calculating the tension of a 1/0 ACSR wire too high. Since the propagation of errors is not necessarily a Linear Function, the calculation of the final result can be thought of to include Generic (possibly not linear) Functions at each stage or category:
Let's review each category in turn to describe how errors can develop.
Nonlinear Sags & Tensions
This is the most critical calculation as it determines the major loads placed on the structure and is the basis for all clearance calculations. There are several aspects that are important to generating accurate tensions and sags:
- You cannot use a fixed tension value for each wire type. Actual wires will almost certainly be in a different situation than whatever the constant value was based upon.
- You cannot use a constant Modulus of Elasticity value for the wire. You must utilize the nonlinear material coefficients for both creep and stretch for all material types used in the wire. It is a fact that all wires have nonlinear material characteristics.
- You must calculate Initial, Final with creep and Final with load values for all possible load cases anticipated. Missing even one required load case could have a significant impact on final tensions and sags.
- You must take into account elevation differences. Typical elevation differences will have a small impact on final tensions, but even more of an impact on clearance calculations.
- You must calculate each and every span. Each different span length and elevation combination for the same wire will have similar tensions under stringing conditions for the same ruling span, but much differently under heavy load conditions. If it is assumed that wire tensions are balanced on each side of a structure under all load conditions; but the span length and/or elevations are different, another error is introduced.
In addition to calculating Sags and Tensions correctly, implementing Load Nonlinearity during Structure Analysis would be difficult to do, or do well, without a clear understanding of how to calculate Sags & Tensions accurately.
Linear Structure Response
This area of calculations covers how the Structure is modeled mathematically to be solved for a Linear Analysis. All accurate methods involve modeling the structure using Finite Element techniques, which breaks the structure down into multiple different elements of different characteristics. The structure model is created from the assembly of the individual elements (represented in matrix form), into a large stiffness matrix used for solving the equation Forces=K(stiffness matrix) * D(displacements).
Modeling of the elements is a way of approximating how that piece/segment of the structure responds(deflects) to forces (includes moments). In the case of tapered poles, for example, an element/segment may represent a length of the pole that is short enough that the diameters of the top and bottom of the segment are not significantly different. This way a segment can be approximated to have a constant diameter for its short length; as one example of approximation. If the tapered segments were allowed to become long, there would be significant error between how the real pole responds and how it is modeled. Other means of modeling tapered pole segments can be much more accurate than this average diameter method. With an eye to using this same Finite Element Model for nonlinear analysis later, one would need each element not to be too long (even if perfectly modeled) in order to better capture nonlinear effects such as P-delta and buckling/stability.
In summary, Finite Element Analysis is the only accurate way of modeling today's complex structures by assembling many well understood sub-elements into a mathematical model for the structure. Some element models are better than others, but the real test is how well they are combined to model real poles in real scenarios. Considering that guying is part of this structure is essential as their reactions cannot be any different than the points of the structure they are attached. They must be solved at the same time and considering them as additional elements of the structure is the proper way. Considering that the soil foundation also deflects when it supports the structure is also "best practice" and further improves the accuracy of exactly how the structure, supported by soil, will respond under load. The soil allowing structure movement is more realistic and therefore more accurate.
It should be noted that a Nonlinear Analysis of a structure involves many iterative Linear Structure Response calculations, which is why this modeling needs to be as accurate as possible.
Nonlinear Structure Response
As mentioned previously, there are three types of structure behavior that can have an impact on the final true results of a Structural Analysis. Both of these go beyond what a Linear Analysis alone can predict:
- Nonlinearity of member reactions due to structure deflection (Geometric Nonlinearity)
- Nonlinearity of loads due to structure deflection (Load Nonlinearity).
- Is the structure stable?
Since these are all real aspects of how a structure may react under load, neglecting any or doing them poorly can be a significant source of error.
The first one, Geometric Nonlinearity means that as the structure deflects and deforms, other loads may be introduced because of the deflection (p-delta) and the 3D stiffness of the structure's members to loads may change as a result of this deflection (e.g. guy angles to anchors).
The second one means that some of the loads may change in magnitude or direction as a result of the structure's deflections. A good example would be a wire attachment that slackens or tightens as a result of the structure's movement.
The third one is critical as it determines if any of the previous Nonlinear results are even valid. If a Structure is in an unstable state, the Structure is unsafe and cannot support the loads required. Most times this will be indicated by excessive structure deflections.
These secondary effects are part of a nonlinear analysis because their impact cannot be determined directly. Their effects are related to the structure's deflection, which is determined by all input loads plus these secondary effects. The end result must be determined through an incremental analysis, looking for the point where the structure's deflection and the secondary effects stabilize. For some poles this point is not reached because the combination of the input loads and the secondary effects is too great for the structure to resist. This also an unstable structure.
The results of a nonlinear analysis will be dependent on how well each of these secondary effects are treated. The input to a nonlinear analysis is the same as a Linear Analysis, and consists of tension results from the Sags & tension calculations (which could have errors) plus a few lesser loads. The nonlinear analysis could introduce errors by itself, but it relies on performing many Linear Analysis operations in an iterative fashion in order to settle on a final answer.
Foundation Response
Last but not least is the analysis of the structure's foundation to see if it can withstand the loads required of it from the structure; as a result of a nonlinear or linear analysis. Many software tools ignore this area totally; which means that foundation failure could occur and result in the failure of many structures whose analysis results were favorable. It is a total error not to test structure foundations to ensure they are capable.
Other sources of error can come from how soil foundation is analyzed in the Linear and Nonlinear Analyses. If the soil was modeled as being perfectly stiff, that is an assumption that is not supported by facts unless it is rock. Based on Soil Class, soil does allow for below grade structure deflections. Taking this into account is the most accurate.
The last source of error for foundations is the methodology used to determine soil capacity the lateral forces, bending moments and vertical load. There are a few methods available. Generally speaking most methods that utilize soil strength parameters for the Soil Class involved should be roughly equivalent and considered accurate.
- Overview
- Understand your Material
- Initial Curve
- Final with Load Curve
- Creep Behavior
- Temperature
- Determine Sags & Tensions
- Get Your Starting Point
- Normal Tensions
- Slack Tensions
- Service Wire Tensions
- Calculations
- After Starting Point
Overview
Determining the specifics of the wire and cable attachments on a pole or other structure, is the most important feature to the analysis of any pole or pole line. The tensions, along with the associated wind and ice loads, determine the loads to be applied to the structure and the sags of the attachment. Knowing the sag of the wire or cable will determine ground clearances and mid-span clearances. It is well established and provable that tension and the amount of sag that results are inversely related. As the tension in the wire/cable increases, the amount of sag that is created is reduced. The reverse is also true. A very approximate relationship has been used for years for a quick estimate of sag or tension, if you know one of the values already:
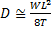
Where:
W = weight per unit length
L = Span length
T = Tension
D = Sag
Failure to calculate the Sag and Tension accurately is the leading cause of differences in the Analysis Results of Pole Line Design software tools. If you have these values wrong or too far off from being accurate, the loading on the structure will not represent reality. These inaccuracies can lead to undetected overloaded conditions or upgrade recommendations which are simply not necessary. There are considerable differences in how different software tools approach this requirement. Some tools expose to users how they calculate Sags & Tensions, while others provide very little insight (Black Box). Of the tools in use in the Marketplace today, many create inaccurate predictions through the use of the following practices:
- Ruling Spans. If a tool calculates an average or Ruling Span and applies it to one or more pole spans, it is not calculating exactly what is required. It is making assumptions about how the structures behave in response to unequal span lengths along a pole line under different loading conditions. These assumptions may not be valid. In the case of Joint Use Distribution Pole Lines, this assumption is almost certainly to be inaccurate. More on this later.
- Pole Elevations. If a tool does not take differences in attachment height elevations into account, the tensions and sags calculated will be inaccurate, period. Elevation differences change the effective span length for the calculations, which changes the tension and sag values that should be used. This will be shown in detail later.
- Constant Modulus of Elasticity. Several tools in the Marketplace use one value for the major parameter of wires or cables – Modulus of Elasticity. This parameter is similar to a spring constant in the way it relates the amount it stretches with the amount of tension. The reality is that no wire or cable that exists has a purely constant modulus. The modulus (slope of the stress-strain curve) changes as more tension is applied. Failure to recognize this will result in inaccurate results, or the correct result by pure luck. Slack Tension situations would be an exception to this as the tensions are very low on the Stress/Strain curve.
- Wire Creep ignored. All wires and self-supporting cables in the Marketplace today will permanently stretch when exposed to constant everyday tensions over a long period of time, or as a result of being exposed to extreme loads. In response to this permanent stretching, the tension in the wire or cable will reduce and the sags will increase. This phenomenon has been well-known for several decades and can result in very different results than if it was not considered at all. Failure to consider this effect can lead to significantly inaccurate results. For wires with more than one type of material (Outer/Core) the effects of Creep must be taken into account separately in order to determine the net impact to the wire.
- Using constant tension values. Some tools require that tensions be pre-determined and entered into a data file for their use. Different tension values are specified for different span lengths and loading criteria for the Loading Analysis stage of their software tool. While there is usually some adjustment to better relate these values to the actual span lengths of the pole line, these can never be as accurate as calculating the Sags & Tensions directly, for the following reasons:
- The amount of permanent stretch (creep) experienced by the wire/cable is dependent on the actual span length. As mentioned above, this has a significant impact on sag & tension. It is unlikely that a simple interpolation of values between the provided span lengths will produce accurate results.
- The amount of wind and ice load that must be extracted from the provided span and tension values for proper application to the pole structure for support must be estimated. This can be difficult, especially when the wind is applied at angles different than 90 degrees to the wire or cable.
Whether you are an experienced Pole Line Designer or a Professional Engineer taking responsibility for the work or someone new to this field, it is important to understand and become completely comfortable with the concepts. With this knowledge you can critique the value of any Sag & Tension result generated by any means.
Understand your Material
In order to have some assurance of accuracy of results, it is essential to understand the material you are using and how it behaves under various circumstances. For Sags and Tensions of wires and self-supporting cables this is very important as they do not behave in a linear fashion. Regardless of the material used (steel, aluminum, copper, fiberglass, Kevlar yarns, etc…) all materials have nonlinear characteristics that significantly impact the final results. This importance is compounded further when more than one type of material is present in the wire or cable.
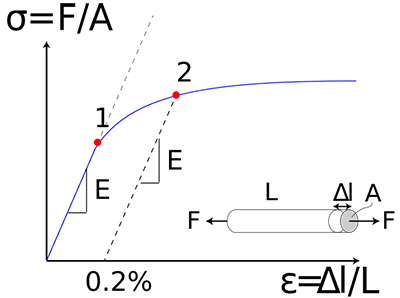
This generic curve shows some important principles that are common to any material you are using:
- There needs to be some amount of elongation of the material/wire/cable in order for it to be under tension; even if it is barely measurable. In the figure above for a sample of material of length L, this is shown as ΔL.
- The ratio of the change in length to the original length is called "Strain".
- The more Strain that exists, the higher is the tension and stress in the material (stress = Force/Area)
- The slope of the Stress/Strain curve at any point (Stress/Strain) is known as the Material's Modulus of Elasticity. It can be evaluated as an average value over a certain range, or at a specific point on the curve.
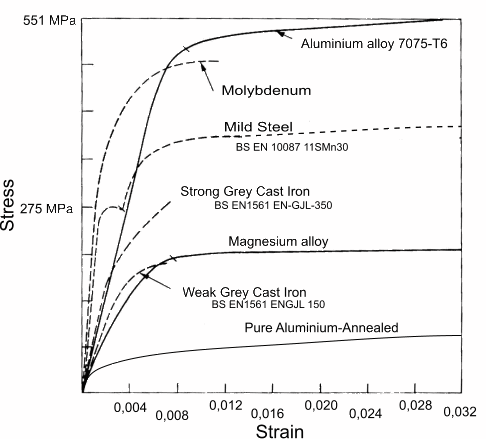 The shape of the Stress/Strain curve for different materials can be completely different. They can useful in providing insight into how the material will behave in your application. Here are a few material examples:
The shape of the Stress/Strain curve for different materials can be completely different. They can useful in providing insight into how the material will behave in your application. Here are a few material examples:
In all types of material there is a region of stress (force/cross sectional area) where the material is almost perfectly elastic. That is, it returns to its original length when the load is removed. Beyond this point the wire/cable will be longer when the load is removed than before it was applied. The material is now permanently stretched. The region of stress in the curve where this permanent stretching happens is called the "plastic" region. Within this region the material can undergo what is called "Strain Hardening", which may allow the material to handle additional stress up to what is called the Ultimate Tensile Strength (UTS), where it breaks. Rated Tensile Strength (RTS) values provided by manufacturers are the guaranteed performance values; which are lower than the expected UTS of individual samples.
Initial Curve
Manufacturers of Wire and Self-supporting Cables for Power or Communication purposes are typically asked to provide fourth-order polynomial equations that describe the product's Stress/Strain behavior. These polynomials are expected to be curve-fitted to actual Stress/Strain test results for validation purposes. This mathematical approximation of the Stress/Strain curves is essential for accurate computer modeling of Sags and Tensions. They are considered valid up to a strain of 0.5%. After that point a straight-line projection (tangent) to the curve is extended, if required. This curve is called the "Initial Curve" as it represents the material's response to initial stresses when first put into service.
Most materials used in Power Conductors, Wires and Self-Supporting Cables will stretch plastically (permanently) if the stress applied exceeds a certain Yield Point. For simplicity purposes, many materials would define this point as the point where the Strain reaches 0.2%; which is cited in many metal testing criteria and ASTM tests. In reality though, this point can vary with material and is only useful for conceptual purposes. Some materials will plastically stretch a small amount under small loads and then much more significantly under heavy loads. Some plastically stretch throughout their Stress/Strain curve, such as most aluminum alloys. After the initial amount of plastic stretch occurs, no further plastic stretch will occur in this same material sample up to the same maximum extent that stress was initially applied. The straight line that occurs after maximum load on any material is called the "Final with Load" curve.
Final with Load Curve
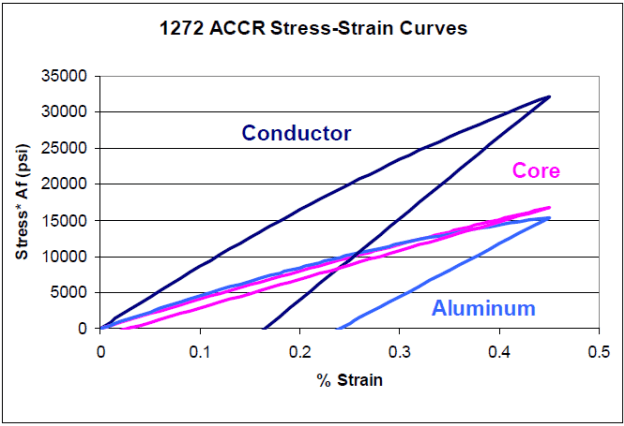 The Final Load Curve is a large contributor to the Sag and Tension results. It represents how the material behaves after it has seen the worst tension and loading condition expected. More on this later.
The Final Load Curve is a large contributor to the Sag and Tension results. It represents how the material behaves after it has seen the worst tension and loading condition expected. More on this later.
Let's look at an example of a 3M 1272 ACCR Conductor: The violet curve shown represents the steel core of the wire. Its upper curve shows the Initial Curve as stress is gradually applied to the core. The lower violet line shows the core's behavior as the stress is removed. It follows the Final Load Curve for the Core. The light blue curve represents the Aluminum outer wires of the conductor and follows the same logic; except it is easier to see the difference between the Initial and Final Load Curves. The dark blue curves show how the core and outer wires, in their proper proportions, may come together to respond as a unit.
Creep Behavior
Another significant behavior of most wire/cable materials is that even modest, everyday tension loads on it will cause some permanent plastic stretch. This behavior is called Creep. Some wires/cables may have been installed for years, but have never experienced the maximum design loads that would have created permanent stretch that way. We must account for this to ensure our design considers this possibility. If a constant tension was exerted onto a material sample for a long period of time, the amount of creep that would develop would be highest in the first few years and then reduce over time to negligible amounts.
Wire and Self-Supporting Cable manufacturers place their materials under tension for 1,000 hours to determine the amount of creep that will occur based on the loads applied. Separate test results are normally generated at 15%, 20%, 25% and 30% of the Ultimate or Rated Tensile Strength of the material. These results are extrapolated on log paper to estimate the amount of creep expected in 100,000 hours (~ 10 years). After this point the additional creep that could develop is considered by the Industry to be so negligible that it is not worth considering any further. The 10 year projection is expressed in terms of a polynomial, similar to the Initial Curves, for ease of use within software tools. This polynomial represents what is called the "Final with Creep" curve for the material.
Temperature
The above discussion on curve creation (Initial, Final with Load, Final with creep) assumes a constant known temperature for the material sample. All materials that are currently used in pole line construction expand with an increase in temperature. Said another way, these materials would have a positive coefficient of thermal expansion. This means that the physical length of wires and cables will increase on hot days or under heavy electrical loads. This is fairly intuitive to most that power wires/cables would sag more on hot days than in the winter. Therefore it is important to consider what temperature to use for the sag and tension result you are seeking.
Determine Sags & Tensions
Now that we understand how a material will respond to changes in loads and temperature, we need to use this to determine the Sags and Tension values we are looking for. The first question then should be "What are you looking for"? Code requirements of the NESC and CSA will identify some design requirements that you need to meet, but can be less specific on how to calculate them. Each code set will specify certain load cases and require that the design requirements of the standard be tested against all possible conditions (for that requirement). The end result is that just one calculation for sag and tension of a wire or cable is always inadequate. Several values must be calculated for evaluation against the various code requirements. For instance, maximum sag never occurs under the same load conditions as maximum tension.
One thing you should note from the Material discussion is that finding the worst load condition (as seen from the material's perspective) is highly important as that helps define the "Final after Load" conditions for the wire or cable. The extent that the material experiences the plastic region of the Initial Curve has a significant impact on Final after Load values. The higher it goes on the curve, the more permanent stretch there will be. The temperature and load experienced under every-day conditions (assumed to be 10°C for most cases), defines the "Final after Creep" values.
So we have three different curves (Initial, Final after Load and Final after Creep) for how this material behaves. Which one should we use? The answer is all three, as the design requirement is to meet the code requirements under all expected conditions. Load conditions plus material conditions. Let's review each of these expected conditions in the material:
- Initial. The day after a wire or cable is strung; it could experience any of the expected load conditions, from no loading to maximum loading.
- Final after Load. The wire or cable may have experienced a maximum loading condition already. Some permanent stretching has occurred.
- Final after Creep. The wire or cable may have never experienced a significant loading event in its lifetime, but has existed for several years undergoing some amount of creep. The actual amount of creep could be anywhere from none (which follows the Initial curves) to a maximum predicted value, dependent on the length of time since it was first installed.
As you can see, you must calculate sag and tension values using all three curves and then test the worst value against the code requirements for all load conditions. This is because the wire or cable could be in any one of these states or some variation of the three. To meet code requirements you must test against all expected conditions in the material and these three curves are the major variations recognized in the Industry all over the world. Determining values using each curve individually establishes the maximum values for that scenario. Since actual wires could be in a state that is a mixture of these scenarios, using the three curves ensures that the worst case condition is always used for testing against code requirements. It also ensures that your design will be compliant with today's code not just for today, but for the expected lifetime of the structure . Since the actual occurrence of specific load conditions are not predictable (since weather is involved), this approach ensures that all realistic scenarios are included when testing against code requirements.
To determine the Creep curve, you must know the stress value expected on the Initial curve under everyday loads (no wind or ice, 10°C; for example). Find this spot on the Initial curve. Then use the creep polynomials to estimate the amount of strain after creep. This will be either equal to (low probability) or greater than the strain value from the Initial curve. Now draw a line through this point that parallels the Final Load curve. The slope of both of these lines is equal to the Final Modulus value for that material, which is provided by the manufacturer. For any load condition expected on the Creep curve that is higher than the point where it intersects the Initial curve, the Initial curve is expected to be followed.
After now establishing the three curves (Initial, Final after Load, Final after Creep), we can now proceed to answer any of the code requirements that we have. Remember, for each requirement we must use the worst value expected of all real load and material conditions. For an example, what is the maximum sag for the wire we evaluated? This would typically be for ground clearance requirements. In essence you need to test all possible load conditions required for code compliance, plus any other you feel are warranted. For this requirement there are a few conditions that are typically the most significant:
- Thermal conditions – the maximum sag at the thermal temperature for the wire of any of the three curves. In this case the thermal temperature may be 100C with no wind or ice. The sag value required is the maximum value obtained from any of the three curves.
- Maximum Sag with Ice at the highest temperature – this is most often a condition where ice is formed on the wire, the wind is low or zero and the temperature is as high as can be expected with the ice still attached. The circulating air can be higher than the wire as it is the wire's temperature, not the air, which determines the thermal elongation of the wire. In many locations this is 0° C, no wind and maximum ice. The sag value required is the maximum value obtained from any of the three curves.
The codes will specify exact temperatures to evaluate some of the requirements, such as mid-span separations of attachments on the same line or crossing over/under others. These may vary based on the type of wire or cable. The same process would be applied for those temperatures and load conditions, looking for the maximum/worst value from all three curves. Although in these examples we were interested in the resulting sag values, the same process and rationale is used when looking for maximum tension.
Get Your Starting Point
The three curves discussed (Initial, Final after Load, Final after Creep) are an integral component of determining the actual Sag and Tension values, but don't provide the values we need easily by themselves. To get started, we need a starting point. That is a known, measurable and verifiable condition along with either a tension or sag measurement. Something you could send a survey crew and possibly a Line Crew with the appropriate tools to measure in the field. This is critical to any calculation as it provides the linkage between reality and the calculations. As you already know, you can take any piece or wire or cable and get different sag values by changing its stringing tension. If you change this starting condition, all other load and material condition tests will yield different results for sags and tensions. So it is critical to know your starting point.
Normal Tensions
The most desirable starting position is the known stringing tension of the wire or cable at a known temperature; assuming new material that was never placed before. You may know these values if they are recorded, or you may have organizational standards that call for stringing tensions at different temperatures for installation crews to use. It is generally accepted that existing wires or cables would have been strung to organizational standards, if no other data is available. This is based on the assumption that installation crews were trained to use these standards and were somehow tested for how close they were able to reach these values both during their training and possibly on different projects over time. Desired tensions can be achieved by several means such as direct measurement using a dynometer, striking the wire and counting the amount of time for reflections to return from the far end, or by using sighting boards which help to achieve the desired amount of sag between poles. Experienced linemen that have used a particular wire for many years are expected to get the desired tensions quickly and consistently; although checking their tension results periodically is also highly recommended.
When applying standard tensions, Installation Crews may have Organizational Standards that vary by the Ruling Span length. Since in any line there will be poles with shorter spans than the average, the Installation Crews are expected to pick which Ruling Span Length to use from the charts they have. This is expected to be a judgment call, mainly based on the area and existing average span lengths. For Communication wires/cables there are usually no differences in the proposed tension except for special applications. For Power Conductors, many utilities have different categories of Ruling Spans such as Service, Urban, Rural and Long-Span rural. Designers should use the same rationale for choosing an installation tension as what they can reasonably expect the Installation Crews to use.
Another interesting point about tensions is that while a conductor/cable may not be completely up to standard installation tensions, it should be expected to be brought up to proper tensions at any time as part of a maintenance activity. The key point here is that designers may not be involved in any re-tensioning activities. Therefore designers should expect that this is a possibility and ensure the line is designed appropriately to allow normal maintenance activities without their involvement.
Over-tensioning is something that may also happen for a variety of reasons. It could occur from excessive tension during stringing operations, or due to excessive re-tensioning of guy wires after normal stringing activities. A good Industry Test Objective to follow is to achieve the tension values within 10% accuracy to the desired values. It is impractical to mandate exact values from installation and maintenance forces. For Design purposes, a designer must assume the plant was strung to normal tensions unless they have knowledge or evidence to the contrary.
Slack Tensions
Another scenario you could run across is a wire or cable that is obviously strung to far less tension than normal. There can be specific design requirements for the pole line that require this, such as poles with no room for proper anchoring. In other cases you may visually notice some obviously slack wires or cables that should be re-tensioned. They could have been subjected to loads that exceeded what they were designed to expect (weather events, traffic accidents…). The pole line may also have some corner and deadend anchors that have pulled somewhat and may in fact be under-sized for the type of soil. In any event, under-tensioned wires and cables that could impact clearances must be addressed through re-tensioning and consideration of the existing anchors.
Slack Span Construction is a technique that can prove useful in dealing with difficult situations, as a last resort. It is prudent for the designer to consider all other options first as pole lines under full tension provide more reliability and are easier to maintain and build.
The good thing about Slack Spans is that you can always assume that the wire or cable is in a "new material" state, regardless of when it was initially constructed. This is because the everyday tension is very low on the Initial Curve and even heavy loads will not create very high stresses on this curve. If everyday tensions are low, long term creep will not be significant. If the wire or cable does not see high stresses, it will fundamentally only operate within the purely elastic area of the Initial Curve. This means that so little permanent stretch from either creep or plastic stretch will have occurred, that the material can be observed in its current state (sag/tension) and assumed to be "new material" for calculation purposes.
To capture the "starting condition" for slack spans, the best way is to estimate the existing sag of the wire or cable. Knowing this value, the span length, the temperature and the relative attachment heights will accurately define the tension (which defines the stress). It can also be advantageous if you have pole survey crews capturing similar data in the area as no other special tools are necessary. You can also directly measure the tension in the wire or cable, however this is usually more time consuming to coordinate and costly. You can also directly measure the tension on existing head-guys, in some situations, and iteratively adjust the tension in a whole-pole loading analysis until you reach values that appear reasonable for the same temperature. Some organizations also having been using some "rules of thumb" which could be very close, or close enough, to the appropriate values to use. For instance, for spans up to 20 meters, an everyday tension value of 100 Newtons (20 lbs.) might be used.
Service Wire Tensions
Service wires to residential and commercial buildings deserve special mention. Most wires or cables used for servicing customers can be run either pole to pole or pole to customer. When run pole to pole they are always tensioned to higher values than pole to customer, as the clearance and separation requirements are harder to achieve over these longer distances. Many organizations have different installation tensions defined for service connections than for mainline attachments. That is part of the answer as those tensions were established to meet the maximum service span length anticipated; which is usually 38 meters.
There is a requirement in the Electrical Codes of Canada (CEC Part 1) and USA (NESC), and perhaps other countries as well, for the power service connection point to withstand up to 600 pounds of combined load, under worst case conditions, from all attachments on the smallest of services from an amperage perspective. This covers residential and many commercial buildings. Larger commercial buildings would have higher tension load capacities with corresponding larger conduit and mast pipe sizes. In many cases, communication drops will attach to this same service mast as power. In other cases, especially commercial buildings, communication attachments have their own support at the building. This is important context as Power Utilities do not want to field complaints from customers if their power mast is pulled off their building. This has driven behavior in installation tensions for spans shorter than the maximum which should be considered.
Like mainline wire and cable attachments, it is convenient and desirable to assume with confidence that specific tensions were utilized at installation time. In the case of power service wires, often only tensions for the maximum span length are provided. This leaves designers wondering what values to use as the maximum values are obviously inappropriate for many typical installations. Also, it is impractical to perform survey measurements on all services when assessing a pole line. There are just too many of them, creating too much of a burden on the pole line owner or attacher to do a detailed accurate assessment. A simpler, but reasonable way is needed to estimate the tensions of power services.
One company in Canada surveyed and measured tensions on many different power service wire installations of various lengths in two different cities. From the results, they analyzed the data collected along with feedback they received from several Canadian Power Utilities on their installation practices. The outcome, which was suspected but not proven before, is that Power Utility technicians do not pull their service wires to full maximum tension unless it is needed for clearance purposes. In almost all cases, vertical sag below the attachment point at the customer's location of about 0.5m was being achieved at installation time. This is consistent with the desire of the power utility to stay well below the 600 pound limitation of most service masts; especially those of older buildings built before this load requirement was well understood. If the designer has no other information to use, the results of this study may prove useful to them. The ability to use this study's results is incorporated into Quick Pole.
Calculations
The above guidance for a starting point in calculations was necessary, but it doesn't set our starting point on the Initial Curve yet. For that you need both Stress (Tension/Area) and strain. A little more work is required. There are three sets of equations that need to be solved simultaneously in order to get this point. One set of equations is the Initial Curve itself, relating Stress (or tension) to Strain (or stretch), defined in polynomial form by the manufacturer:
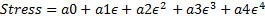
WhereThe second equation is recognition of the thermal expansion coefficient for the material:
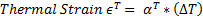
Where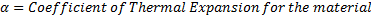
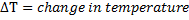
The third equation ensures that the wire or cable solution fits the physical restrictions placed upon it such as the specific span length, relative attachment heights, temperature and either a measured tension or a measured sag.
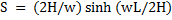
Where
S= wire or cable length between attachment points
H = horizontal tension at maximum sag point
W = load per unit length
L = effective span length
 It can be shown that this formula must be true for any wire or cable that has a constant weight per unit length along the span.
It can be shown that this formula must be true for any wire or cable that has a constant weight per unit length along the span.
These three equations that define the behavior of the material and its physical restrictions are then solved, usually in an iterative manner, to land on a solution that satisfies all three. There are several methods available to software providers, some better than others.
A complication to this calculation exists when there are two types of materials in a single wire or cable. A common example is a 1/0 ACSR wire (aluminum covered steel reinforced). The three curves and thermal coefficients of both materials are all different. In these cases, the restrictions on both the core and outer materials must be satisfied at the same time. There is a manual graphical way of calculating these simultaneous equations that was developed by ALCOA many years ago. It is seldom used these days, but is still valid for any interested reader. What software tools can do for the user today is amazing compared to the manual processes of the past.
After Starting Point
After you have your starting point on the Initial Curve you must then apply all reasonable load conditions to the wire or cable to find the one that stretches it the highest on that curve. This helps to define the Final after Load curve. You also need to determine where on the Initial Curve the average everyday "No Load" at 10C condition would lie. You need to specifically calculate the stress of this condition. From this you can solve for the applicable strain value after Creep from the Creep polynomial. Following this stress and new strain value down to zero strain using the slope of the Final Modulus of Elasticity will determine the amount of permanent stretch due to creep and the Final after Creep Curve.
This process will need to be done for every different material type within the wire or cable. Once these three curves are well defined, all other load conditions required by code (plus other reasonable or desired ones) should be tested and made available. Then for each code requirement, as mentioned before, the results from all three curves must be considered under all reasonable load conditions.
As mentioned previuosly, maximum sag and maximum tension will not be from the same load case. Each span will need to be calculated separately to uniquely consider the span length and elevation differences.
- What is Nonlinear Analysis?
- Geometric Nonlinearity
- Material Nonlinearity
- Load Nonlinearity
- Boundary Condition Nonlinearity
- Summary
What is Nonlinear Structural Analysis?
In simplest terms a Nonlinear structural analysis is one that considers other secondary effects that may have an impact on the structure's response to the loads applied. In comparison, a Linear Structural Analysis does not consider the possibility of any secondary effects. The most well-known nonlinear structural effect is P- Delta; vertical loads on a leaning pole causing additional bending moments.
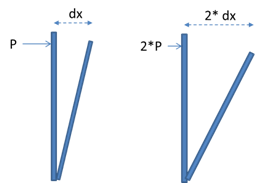 Understanding linear structural analysis will facilitate a better understanding of the Nonlinear method. There are several methodologies that fall into the linear category, but they all have one thing in common. In a linear structural analysis, the structure is assumed to be perfectly elastic and totally linear in its response to forces.
Understanding linear structural analysis will facilitate a better understanding of the Nonlinear method. There are several methodologies that fall into the linear category, but they all have one thing in common. In a linear structural analysis, the structure is assumed to be perfectly elastic and totally linear in its response to forces.
This means that if a given force was applied to a portion of a structure and it deflects a specific amount; doubling the force should generate twice the amount of deflection. This enables, for linear analysis, the principle of superposition of forces. You could analyze the response of the structure to each force individually and add up (superimpose) all of the calculated deflections (or stresses) to arrive at a final response for the structure. The simplicity of this method is very attractive.
The linear methodology assumes many factors which may or may not be accurate. For this reason the linear methodology has required higher load and safety factors by some National codes in the past to account for these assumptions. In Nonlinear methodology, the primary assumptions used in the linear methodology are considered and addressed. The end result is a much more accurate estimation of the structure's response (deflection, stress, etc.).
With the use of linear methodology, the possibility of the structure becoming unstable had to be evaluated separately from the loading analysis. It is conceivable that a specific linear analysis could show that the structure's components are well below yield point stresses, yet the total structure could be in a failure state. For example, to estimate the stability of a single pole structure to resist vertical loads, Euler's buckling formula was modified by Gere and Carter to take a single pole's taper into account. This in itself is still just an estimate with its own set of assumptions factored in. The principle assumption is that no attachments offer any stability to the pole along its length. Structures consisting of more than one element (i.e. most Transmission Structures) are very difficult to analyze using linear methodologies.
In Nonlinear Structural Analysis, the stability of the structure is determined as part of the complete solution procedure. Structures that are not stable simply do not converge on a final solution or the determined deflections are that of a collapsed structure.
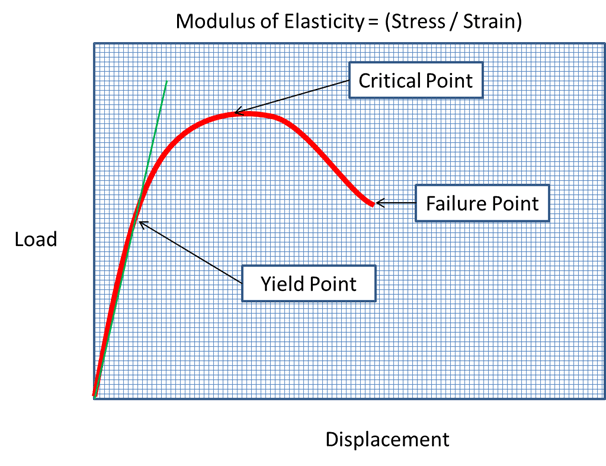 As loads are initially applied in small amounts to a structure, the structure will respond in an approximately linear manner. At some point, other (secondary) effects begin to influence how the structure responds. This occurs at a point that can be referred to as the Yield Point for the structure, which is similar to the Yield Point of most metals. As the loads are increased on the structure, these secondary effects will become very significant and the structure is said to 'soften' or become less stiff. Once the loads reach what is called a Critical Point, the structure will no longer be able to resist the loads. The result is rapid displacement of the structure components towards the Failure Point where the ultimate failure of the structure and its materials occurs rapidly. In other words the structure collapses or buckles.
As loads are initially applied in small amounts to a structure, the structure will respond in an approximately linear manner. At some point, other (secondary) effects begin to influence how the structure responds. This occurs at a point that can be referred to as the Yield Point for the structure, which is similar to the Yield Point of most metals. As the loads are increased on the structure, these secondary effects will become very significant and the structure is said to 'soften' or become less stiff. Once the loads reach what is called a Critical Point, the structure will no longer be able to resist the loads. The result is rapid displacement of the structure components towards the Failure Point where the ultimate failure of the structure and its materials occurs rapidly. In other words the structure collapses or buckles.
The following sections are all the possible secondary effects that are commonly associated with the term "Nonlinear Structural Analysis" with commentary on how applicable they are to Transmission and Distribution Line Structures.
Geometric Nonlinearity
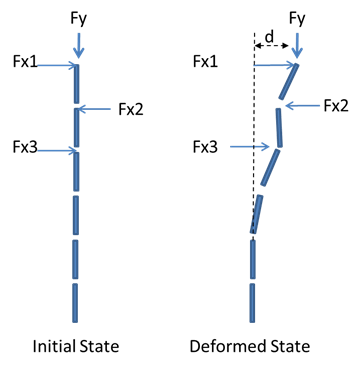 As a structure deforms/deflects in response to the loads applied to it, the fact that the loads are essentially moved to a different absolute location will change the real loads being applied to the structure. The magnitude and direction of the structure's deflection at loading points will in itself introduce additional loads for the structure to deal with.
As a structure deforms/deflects in response to the loads applied to it, the fact that the loads are essentially moved to a different absolute location will change the real loads being applied to the structure. The magnitude and direction of the structure's deflection at loading points will in itself introduce additional loads for the structure to deal with.
For any structure that is expected to stay stable and fixed in one place (all Transmission and Distribution structures), the equations of equilibrium apply to all forces and moments at every point along the structure. So if a vertical force is displaced horizontally, the structure must resist with the appropriate amount of counter-balancing forces and moments in order to completely compensate for this effect. The example shown above in the deformed state is what is commonly called the P-delta effect where the force (P or Fy) times the distance (delta or d) represents the high-level estimation of the bending moments that the structure must resist, over and above the initial loads.
The two-dimensional example above hints at some of the details of this calculation. Of course real structures are three-dimensional and they are exposed to other forces in different directions that are displaced in directions that also create additional moments. Although a single-pole structure is depicted above, these same effects exist in multi-pole, truss and other structure types as well.
Another Geometric Nonlinearity occurs to structure members, including downguys, since their three dimensional stiffness factors change with structure deflection.
It is almost a certainty that all structures will be modeled using Finite Element techniques as part of any Nonlinear analysis. This is a technique whereby the structure is modeled into many discrete elements which are then combined (based on the structure's geometry) into a larger model for the entire structure. The objective is to create a model that can satisfactorily "estimate" the overall structure's response. Its strength is the ability to model even very complex structures using simple, well understood elements. Generally, the more elements provided in the model, the more accurate will be the result.
The discrete elements are individually modeled (in matrix form) for how they respond to forces in three dimensions.
[F] = [k][d]
F = forces
k = element stiffness
d = local displacements
If an element's properties change with length (e.g. diameter of a pole) or its length is significant, best practices would suggest that an element be broken up into additional smaller elements. This will help provide a better estimate in element and structure responses.
In order to model an entire structure with a collection of element models, they are combined into a much larger model in a way that ensures the structure is statically determinant at every element boundary (sum of the forces and moments are zero). Applying the assumed loads at the element boundaries to the larger structure model will allow the calculation of global structure displacements, which in turn can be used to determine local element displacements and reactions (forces, moments, stresses). At this point you will have the calculation result based on a Linear Analysis. The models used assume a linear elastic response within each element and do not yet have any secondary effects included. It is however a necessary first step to get this initial estimate of structure and element responses.
The Geometric Nonlinear effects (such as p-delta) can now be estimated with known forces and displacements and then combined with the assumed loads into the structure model and calculated once more. This provides the first estimate of how the structure will respond to both the assumed loads and these secondary effects. The structure may now have deflected further or in different ways than initially estimated. The secondary effects should be re-calculated and re-applied to the structure model at least once more. This process continues until the deflections of the structure do not materially change, or it is obvious that the structure is unstable. If the applied loads are very close to, but not past, the Critical Point, it will take many iterations to reach a solution. If the structure is already past the Critical Point, these iterations will not converge on a solution.
All Nonlinear solutions must be solved iteratively as there is no way to combine Geometric Nonlinear effects into the structure or element models to solve in one calculation. Other secondary effects can be combined at each iteration step of the solution procedure discussed here, for efficiency. Given the large amount of matrix manipulation and the iterative procedure required, computer software tools are commonly used.
Material Nonlinearity
When the term "Material Nonlinearity" is used in Structural Analysis, it always refers to the stress-strain characteristics of the material or, how the material responds physically to external forces, or force over a specific area (Stress=Force/Area).
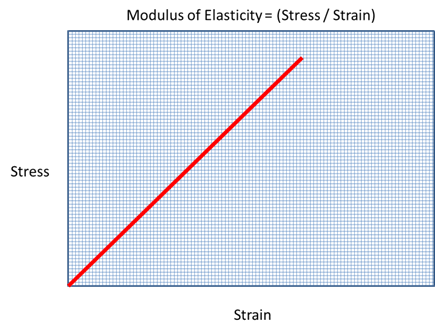 Perfectly elastic materials are said to have a constant Modulus of Elasticity because they respond in a linear manner to changes in Stress. This is recognized by a constant slope of the material's Stress/Strain curve.
Perfectly elastic materials are said to have a constant Modulus of Elasticity because they respond in a linear manner to changes in Stress. This is recognized by a constant slope of the material's Stress/Strain curve.
A Nonlinear material will have a stress/strain response that varies with the level of stress applied.
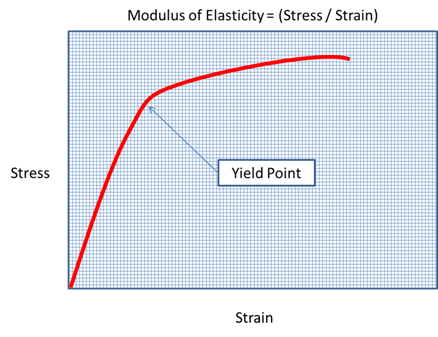 When one thinks of Nonlinear materials, one often thinks about metals and the fact that they begin to permanently stretch after a certain stress level. This is the case for most metals after or near their Yield Strength. There are many other materials that exhibit Nonlinear behaviors as well. Their exact behavior may be influenced by its current deformed state and possibly past history of deformation activity. Other influencing factors may include: pre-stressing, temperature, time, moisture, and electromagnetic fields.
When one thinks of Nonlinear materials, one often thinks about metals and the fact that they begin to permanently stretch after a certain stress level. This is the case for most metals after or near their Yield Strength. There are many other materials that exhibit Nonlinear behaviors as well. Their exact behavior may be influenced by its current deformed state and possibly past history of deformation activity. Other influencing factors may include: pre-stressing, temperature, time, moisture, and electromagnetic fields.
Structure Materials
With respect to Transmission and Distribution Structural Analysis, most common materials used in their construction (e.g. Wood, Concrete and Steel Poles, H- structures, steel truss towers…) can be assumed to respond in a linear manner to external forces, at the element level. This assumption is used to enable the efficient analysis of the structure, followed by confirmation of this assumption by the Designer. This confirmation can be done by determining each element's maximum stress level and comparing it with the Yield Point for the material used in the element. If a certain material is used in a structure that has some Nonlinear properties, the most common practice would be to use updated element models in the iterative Nonlinear analysis procedure.
Attachment Materials
The Nonlinearity of wire and cable attachment material needs to be considered in order to accurately determine the initial loads applied to the structure. These loads may need to be re-calculated as part of Force Nonlinearity (below).
Foundation Materials
While rock can be considered to be very solid, other types of soil will exhibit plastic behavior if they are excessively loaded past their Yield Point. This Nonlinear, plastic behavior is dependent on the soil's cohesive and non-cohesive properties, plus how much stress is applied to the soil in order to resist movement of the structure. Limiting soil stresses below the Yield Point is the common practice so that these factors can be ignored.
Load Nonlinearity
If the assumed loads that are applied to the structure in the analysis can change due to movement or deflection of the structure, this can be an important secondary effect. The loads are said to be Nonlinear as they are neither constant nor predictable separately from the structure. When Load Nonlinearity is considered during Structural Analysis, the loads applied to the structure are normally adjusted iteratively throughout the Nonlinear Analysis.
These effects are very applicable to Transmission and Distribution Lines, but primarily to Distribution Lines as their span lengths are shorter. Over a shorter span, the deflection of the structure(s) will have more of an impact than over a longer span. The primary application that creates Load Nonlinearity for Line Structures is from the various wires under tension that may be attached between structures. The tension forces that are applied to the structures will change in both magnitude and direction as their supporting structures deflect. Since the structures deflect in response to all applied loads, determining the final structure deflection and internal loads is therefore an iterative process.
The following example will demonstrate. A structure with the tension T of one wire attached to another structure a distance of approximately L away is under study. The structure is subjected to wind load on itself and the apportioned wind load from the wire.
Starting Condition
 In this initial condition it is assumed that the structure has no deflection when the forces are initially applied:
In this initial condition it is assumed that the structure has no deflection when the forces are initially applied:
- Fx = T
- Fy = Wind
- Wire Length = L , based on the span length between the structures and the installation tension.
Initial Response

The structure deflects in response to the loads that were applied. It moves away from the wind that was applied and pulled slightly towards the tension in the wire. The wire length is now shorter than it was before, as the structure has now deflected towards the wire exerting the tension. This reduces the tension T to T – dt. The direction of T has changed slightly as well with the introduction of a small angle Θ to the horizontal.
Secondary Response
The loads have now changed as the angle and magnitude of the Tension T are now different.
- Fx = (T – dt)* Cos Θ
- Fy = Wind – (T – dt) * SinΘ
- Wire Length = L - dl
The effect of the angle Θ on T producing some Y direction forces will tend to help support the structure against the wind forces. The structure will no longer need to support the entire Wind load, so it does not need to deflect as much as it did initially. The reduction in tension of the wire will reduce the amount of pole deflection in that direction, as well.
Additional Responses
The adjustments to the net forces acting on the structure will result in less deflections overall.
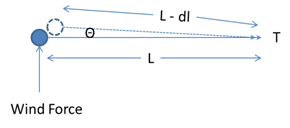 This process of force adjustments is iterative until the structure's deflections stabilize.
This process of force adjustments is iterative until the structure's deflections stabilize.
These Load Nonlinearity effects are most often used in the following scenarios to more accurately estimate the structure and attachment responses in the following scenarios:
- Uneven span lengths on a tangent pole line.
- More wires coming to the pole than are going towards the next.
- Anchor/guy combinations that are not in the ideal location/angle.
Boundary Condition Nonlinearity
This category of Nonlinearity refers to the possibility that the points where the structure is fastened, may move, deflect or rotate. Where most structures are fastened to the soil or rock through embedment or other fasteners, it would be rare that this aspect of Nonlinearity would need to be considered for aerial structures used in Transmission and Distribution lines. This is based on the assumption that the foundation for the structure has been designed to be adequate to support the assumed loads that the structure requires and that the possibilities of foundation movement (e.g. washouts) have been considered.
Summary
The Nonlinear Structural Analysis of Transmission and Distribution structures is an advancement in analysis techniques for Utilities in general. The technique has been taught in Universities and used in other engineering disciplines for many years. It is a tried and proven methodology that Utilities can use to get the best estimation of structural response.
As noted above, Material Nonlinearity and Boundary Condition Nonlinearity of Structures are not normally a concern for Utility Designers. Geometric and Load Nonlinearity are the two aspects of Nonlinear Analysis that are the most important to consider in the design of Transmission and Distribution structures.
What Wood Pole Data is used in Quick Pole?
 Quick Pole is being sold in both the US and Canada today, which makes it very important that it addresses any differences in standards in those two countries. In particular, the standards related to the classification of poles will be discussed here.
Quick Pole is being sold in both the US and Canada today, which makes it very important that it addresses any differences in standards in those two countries. In particular, the standards related to the classification of poles will be discussed here.
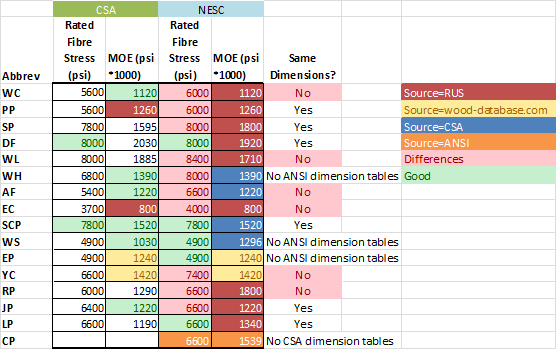
At one time the ANSI O5.1 and the CSA O15 standards were highly aligned. Over time with the inclusion of more pole species and the evaluation of different testing results, these two standards became different. Not only did the rated fibre stress become different in the two standards, but a few pole species started to have different measurements defined for the same pole class. Where many pole manufacturers ship poles across the border, it was always desirable to "Class" a pole the same way so that buyers and designers always knew what they were getting.
This unfortunate reality of different ratings and dimensions for the same class of pole needs to be detected and handled by any Line Design software tool. In Quick Pole this is handled behind the scenes based on the "Line Grade" that is selected for the project. An NESC Line Grade will generate US-based pole parameters while CSA Line Grades will use Canadian values.
The other reality related to US and Canadian standards on wood pole classes is that not all the information is provided that is needed in order to use Quick Pole or any other advanced Line Design software tool. The data that can be missing is the Modulus of Elasticity for the species of wood in the pole. The CSA Standard provides many values (but not all), while the ANSI standard has no recommended values beyond some adjusted values within test results. While some Linear Analysis methods in the past (Groundline moment method...) did not require this value, it is absolutely required for Quick Pole to even do its Linear Analysis on a pole, since it uses Finite Element Analysis for that.
The Modulus of Elasticity is a measure of how flexible or stiff each pole segment is along its length. Knowing this stiffness is critical for any advanced analysis to properly determine the loads that the pole segments, guys and wire attachments will be asked to handle. An assumption for the missing values had to be made in order for Quick Pole to function. While it is thought these are reasonable until the respective standards are updated to suggest new values, the onus is on the Designer to ensure that these are accurate enough to use.
Preface
This article is being prepared to help guide Professional Engineers being asked to certify or "accept with conditions", the results that are generated from specific Pole Line Design software tools. The focus of the document is dedicated to items of an Engineering nature that a P.Eng could be asked to sign-off on potential projects. Topics related to software cost or user productivity are purposely excluded. This article is very specific to items related to Pole Line Design and is similar to other more general discussion articles around the use of software by Professional Engineers.
Introduction
Pole Line Design Software can have an important role to play in the approval of projects by a P.Eng. The engineer could decide to evaluate and/or approve a specific project with complete/partial or no support from any software tool or manual calculations. They can equally decide to use multiple methods and/or tools in order to fulfill their engineering obligations. The options are almost limitless and only bounded by personal preference, access to tools and/or organizational requirements.
The requirements for the final outcome are that the engineering due diligence has been applied to a project appropriately, in a manner that the engineer will support and stamp if necessary. In any event, they are putting their reputation on the line.
In order for an engineer to do this, they must understand or otherwise be comfortable with the results of any tools or processes they utilize, what they address and also what they do not address. All three aspects are very important. They are also responsible to verify the properties of all materials used in the structural models (pole, guying, soil…), the properties of the wire attachments placing loads on the structure and have an understanding of how all these properties influence the results of the analysis. Ideally a supplier of Pole Line Design Software should assist in some way to make these determinations easy to accomplish, or proactively provide them for an engineer to review. A user manual detailing the strength calculations and loading parameters of the structure would be helpful. As always, ultimate responsibility will rest with the Professional Engineer for the correct use of tools they use.
Discussion
The process of designing new pole lines or assessing existing lines for potential new attachments can be complex and the software used for Pole Line Design may assist with one or many parts of this process. This article provides recommendations related to code compliancy and engineering due diligence only.
Code Compliancy
There are several key areas where codes (such as CSA and NESC) provide specific requirements; most notably:
- Clearances and separations
- Storm and other assumed loads
- Load Factors
- Strength Analysis of structures:
- The Structure itself including internal strength members and guying,
- Things that support the structure (anchors, foundation, soil)
- Strength Factors
The software supplier should provide sufficient information to the approving engineer to make them comfortable with the methodologies used for assessment or that the results are consistently accurate. Ideal responses would provide direct proof and/or easy instructions to follow by an engineer to validate what the supplier provides. The user manual of the software should detail how each of the usages and capacities of the members are calculated.
The software supplier should have a procedure in place to check their software on many common scenarios through a regression of examples such that when new versions are released the results would be verified to not change. If results have changed between versions they should be explained with a change log or remedied before release.
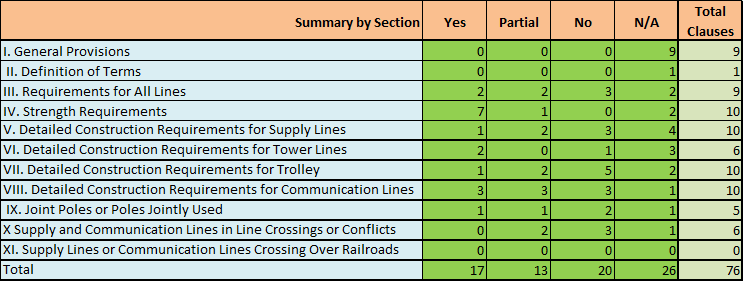
The software supplier should clearly identify what National and other codes that their software supports. For each of these codes or standards, a detailed list of the various clauses should be provided with a statement about compliancy for each one. (Yes, No, Partial):
- Partial responses should be fully explained as to what is covered and what is not.
- Yes and No responses may provide further explanations for clarity.
With all codes it is upon the engineer of record to interpret the requirements of the code and make sure the software meets their interpretation of the code. Code checks supported in the software should be documented in the user manual or supplemental material supplied by the software provider.
Unwritten Requirements
There are some concepts that some codes do not spell out explicitly, but are expected to be addressed, through tools or otherwise, by competent engineers. The extent that Pole Line Design Software Tools cover these is important for an engineer to know and for suppliers to report.
- The first one is that all clauses in the code need to be satisfied. This means that the final design solution needs to consider the worst case scenario for each individual clause. In other words, the worst case scenario to address one clause may not be the right choice for another. The supplier should either indicate what scenario would be used (alternatively how it would be chosen) to address each clause, or provide the means for the engineer to choose the scenario themselves.
- The second one is related to weather/storm loads. Both NESC and CSA codes require that the wind direction be chosen to result in the maximum load applied to the structure and its supports (guys, anchors, pole braces, internal members). In other words – wind can come from any direction, so be sure to evaluate the worst condition. For simply supported poles this means just one direction. For more complicated poles, additional wind directions will need to be evaluated to be sure that each component (guy/anchor) experiences its worst condition as well. Since the wind can come from any direction, it is possible that wind directions where the structure is more lightly loaded could cause higher loads in some of the guys and anchors.
- For Deterministic Storm Loadings, it is implied that the required amount of ice loading at the freezing point with no wind is an additional load case that needs to be considered. This is primarily for clearance tests as it may be the maximum sag condition. The applicability of Extreme Wind, Extreme Ice, and Ice with Wind Loading should be considered.
- The base elevation of poles and changes in attachment heights along the pole line can impact clearances, separations, sags and tensions. Therefore, the most accurate results are obtained when the actual geometry of the line is used in the analysis of structures.
- The materials used in wires for span attachments generally have a non-linear Modulus of Elasticity. Therefore the permanent stretch possible in certain wires under creep or under load can impact the design values used for Sags & Tensions.
- Maximum Sag and Maximum Tension Load Conditions for span attachments are rarely the same.
- There is more than one type of Nonlinear Analysis that can be performed on Structures. The more nonlinear considerations utilized, the more accurate will be the final result. Some codes have minimum requirements for non-linear considerations. If a supplier's software performs a Non-linear Analysis, it should clearly identify the extent of the Non-linear considerations; including but not limited to:
- Non-linearity of member reactions due to structure deflection (Geometric Non-linearity)
- Material Non-linearity of Wire attachments (Non-linear Sags & Tensions)
- Material Non-linearity of Guy attachments (Stretching of guy wires under load)
- Non-linearity of loads due to structure deflection (Load Non-linearity).
- Non-linearity/flexibility of attachment supports .
- Overview
- Code Compliance
- About Sags & Tensions
- Level Spans
- Un-Level Spans
- Unguyed Structure Response
- Model Tests
- Guyed Structure Response
- Model Tests
- Nonlinear
- Geometric Nonlinearity
- P-Delta Model Tests
- Guying Nonlinearity Model Tests
- Attachment Load Nonlinearity
- Model Tests
- Foundation Analysis
- Soil Reactions
- Vertical Load Capacity
- Lateral Load Capacity
- Uplift Capacity
- Model Tests
Overview
Quick Pole has been tested in its abilities and this section's purpose is to show you what we have tested and how our test results line up with another leading Pole Line Design software vendor that has the same breadth of capabilities (we could find only one).
At Sonideft we believe that this should be public information and that users and prospective customers should not need to contact sales people nor sign documents before viewing. The more we can openly show Quick Pole's abilities, without obligation, the more educated prospective customers will be when they compare Quick Pole to similar software tools.
This validation is broken down into various sections for simplicity:
- Sags & Tensions
- Unguyed Structure Response
- Guyed Structure Response
- Nonlinear
- Foundation
Statement of Code Compliancy
Quick Pole can be used to assist in Pole Line Design requirements in many different jurisdictions and possibly local requirements. To assist the Designer in meeting code requirements, we have spent the time and reviewed in detail, three major code standards used in North America for compliance: CSA (Canada), NESC (most of USA) and GO 95 (California).
Common to all three code standards is the fact that the Designer is a major component and that no software tool can ensure that 100% of the requirements will be met or reviewed for compliance. At Sonideft we think it is important to clarify for Designers exactly what is and what is not being addressed by the software tool. That way they will be clear on what aspects they need to consider themselves.
For each code standard, we have reviewed each clause to assess whether Quick Pole addresses the requirement fully, partially or not at all. On several clause items we clarify any specifics required to address the clause, or the extent to which it is covered.
CSA
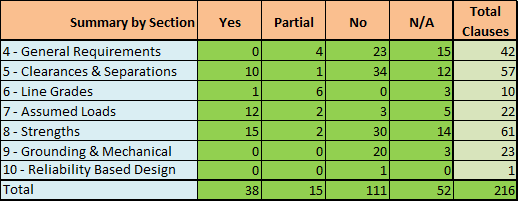
View the complete code compliance report
NESC
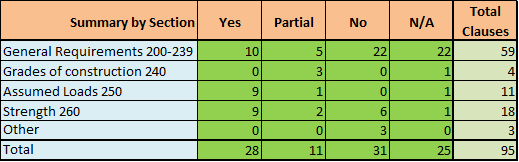
View the complete code compliance report
GO95
Sags & Tensions
The maximum tension and maximum sag of a wire attachment are required to feed the structural analysis and clearance processes, plus to address some code requirements directly. The maximum tension condition will be one of many weather conditions that a tool is expected to evaluate. It should not be assumed to be the worst storm condition as sometimes low temperature conditions can generate even more tension.
As a guide, the following conditions would be expected to generate calculation results:
- Maximum storm conditions.
- Storm conditions at the freezing point and with no wind. This is an ice loading only scenario.
- Various temperatures from the lowest temperature expected up to the thermal limit required in the code.
- Other weather conditions dictated by the structure owner.
- Nonlinear load and creep material characteristics (extremely rare not to be present).
Level Spans
A software tool should be evaluated to see how it can address a wide range of wire attachment scenarios to provide clarity to its abilities. For Joint Use Distribution Pole Lines, the following variations are suggested:
- Wire attachments of different types (single material type and double material type), such as:
- Aluminum wires
- Copper wires
- Steel wires
- Combined Steel & Aluminum wires
- Various sizes of wires:
- Small
- Medium
- Large
- Various span lengths
- 40 meters
- 80 meters
- 120 meters
The following wires were chosen for this evaluation:
 All of the above variations should be tested under level span conditions with wind (if applicable) applied at 90 degrees to the span. Both the maximum tension and the maximum sag should be extracted from these results and compared to the baseline. It should be obvious in the results how to determine:
All of the above variations should be tested under level span conditions with wind (if applicable) applied at 90 degrees to the span. Both the maximum tension and the maximum sag should be extracted from these results and compared to the baseline. It should be obvious in the results how to determine:
- The Horizontal guy-able load
- The Vertical load
- The Lateral load due to wind (if any).
- The Tension at each pole
Level Span Tests
Here are the Test Results from Quick Pole and the required comparison with another leading software tool:
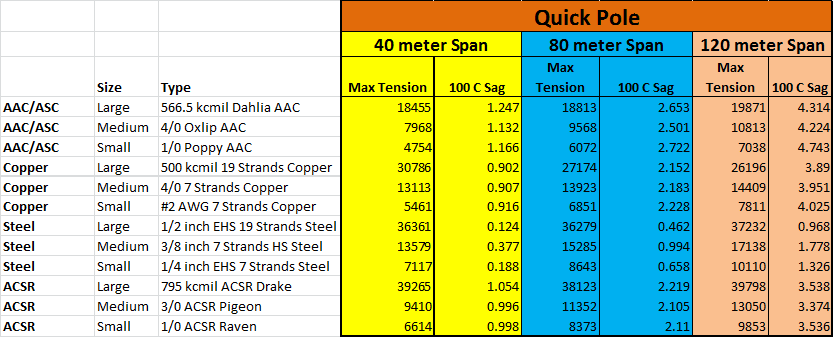
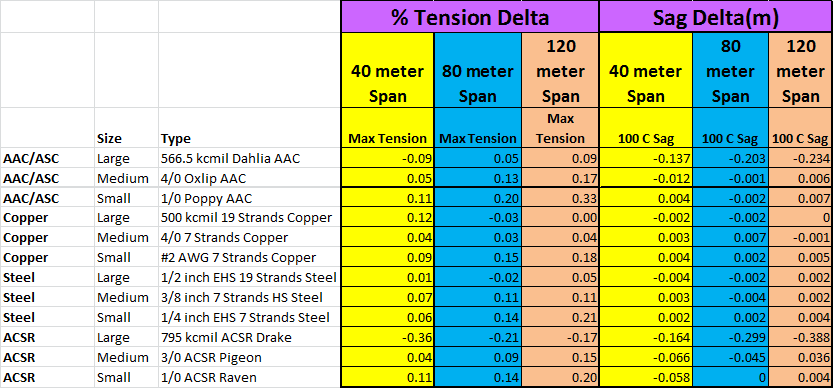
Download the Quick Pole project file to duplicate the results shown above.
Un-Level Spans
 Many situations exist where the Groundline elevation of the structures or the wire attachment heights are different. This creates a situation where the maximum sag point is no longer exactly mid-span and the tensions at both ends become different. Since many code clauses have requirements for mid-span clearances and separations, the possibility that the attachment of a wire is higher at one end than the other should be taken into account for the least error. If a software tool cannot address un-level spans, the supplier should note this in their compliance matrix.
Many situations exist where the Groundline elevation of the structures or the wire attachment heights are different. This creates a situation where the maximum sag point is no longer exactly mid-span and the tensions at both ends become different. Since many code clauses have requirements for mid-span clearances and separations, the possibility that the attachment of a wire is higher at one end than the other should be taken into account for the least error. If a software tool cannot address un-level spans, the supplier should note this in their compliance matrix.
The ability of a software tool to handle un-level spans can be demonstrated with fewer tests than required for basic Sags & Tension calculations. The following tests are suggested:
- One medium sized wire from each of the Level Span categories and using the same stringing condition.
- 60 meter span, CSA Heavy Loading condition
- Attachment Point elevation differences:
- One meter
- Three meters
- Reporting of the following results:
- Maximum Horizontal Tension under CSA Heavy Loading
- Maximum Vertical Load on both supporting poles; under any condition
- Maximum Vertical Sag value and the distance from the lowest pole where this occurs; under 100 °C assumed Thermal conditions
Unlevel Span Tests
The results of Quick Pole have been compared with another leading software tool and found to be in very close agreement.
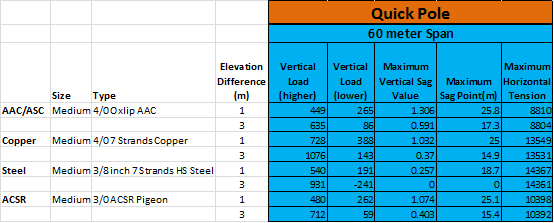
Download the Quick Pole project file to duplicate the results shown above.
Unguyed Structure Response
The focus of this category of tests is to confirm that the basic pole model behaves as expected to create the correct deflections and stresses from known input loads. Testing both deflections and stresses are critical in evaluating if Pole Loading Results "reasonably represent how a real pole behaves". In addition, the amount of stress created for a specific amount of deflection is a key indicator that the "Stiffness" of the pole segments are accurate. The relative stiffness of the pole segments in relation to the location of the applied loads and the stiffness and location of guying, are the major items that determine the pole's behavior along its length (stresses & deflection).
It is assumed that all software tools utilize Finite Element Analysis. That means that the pole is assumed to be modeled into many different pole segments and assembled together to represent the whole pole. The tests listed here will validate that these assembled pole segments do in fact come together and are modeled accurately enough to provide reasonably accurate results. This model is tested across the longest distance possible of the pole in order to ensure any model inaccuracies are exposed that may not appear on shorter distance tests.
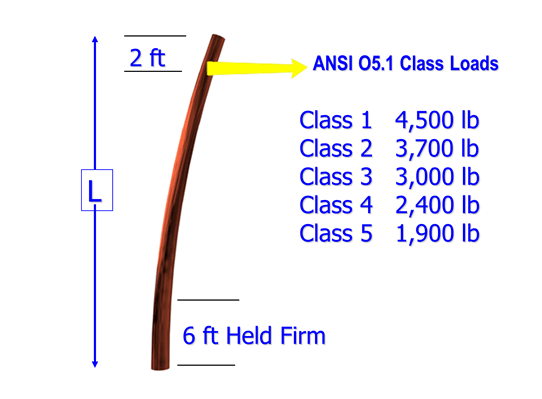 Most of these tests were modeled after the Pole Class Definitions in the ANSI O5.1 standard. The amount and location of the applied load matches exactly with how the pole classes were defined to create its dimensions. This means that the fibre stress utilization should be very close to 100%, recognizing that the pole dimensions for the groundline were rounded to the nearest 1/2 inch.
Most of these tests were modeled after the Pole Class Definitions in the ANSI O5.1 standard. The amount and location of the applied load matches exactly with how the pole classes were defined to create its dimensions. This means that the fibre stress utilization should be very close to 100%, recognizing that the pole dimensions for the groundline were rounded to the nearest 1/2 inch.
In some cases the CSA 015 standard suggests lower maximum fibre strength ratings and slightly different dimensions for the same pole (refer to Pole Data). For this reason one of these tests will be dedicated to a CSA standard-based pole to ensure that the software can properly address Canadian as well as US poles.
Model Tests
It is important to validate that the pole model does not produce different results when loads are placed at different angles and that the results change appropriately to different lengths, classes and species of pole. It is also important to ensure that the pole's deflections and stresses are consistent with each other and the established baseline.
The following tests are suggested:
- Use a 40 ft pole; class range: 4 to 1 dimensioned and rated in accordance with the ANSI O5.1 Standard. Species to be Red Pine
- Apply to each pole, the published rated load for the Class at 2 feet from the top of each pole.
- Repeat the above with the applied load shifted by 90 degrees.
- Using western Red Cedar poles of lengths 45 ft, 50 ft and 60 ft. and for classes 2 and 3, repeat the above tests but from one direction only. Use the same Depth of Setting.
- Evaluate a 40 ft class 4 Red Pine pole using dimensions, strength and Modulus of Elasticity values from the CSA standard. This confirms that CSA values can be used in Canadian designs.
- No wind or storm loads
- Measure the Pole Top Deflection and the Fiber Stresses at the Groundline.
- Depth of Setting is to be 6 feet (1.828 meters) for all tests.
- This is a Linear Analysis with loads applied without additional load factors applied. If non-factored loads are not possible, divide the proposed load by the load factor before it is applied to the pole.
- Constant Fibre Strength and Modulus of Elasticity at all points along the pole are required and should match the published values in ANSI O5.1 standard, CSA Standard and RUS sources (refer to the Wood Pole Data section for more information).
These tests are very important since they test a software's Finite Element Analysis Model. In these specific tests however, direct solutions through formulas are possible assuming round tapered beams modeled the same way.
Even though the ANSI and CSA poles often have different fibre stress ratings, as long as the pole dimensions are the same, a different Modulus of Elasticity has no impact on the resulting Groundline Fibre Stress values. This is because the Groundline Moments are the same (a basic statics computation); so as long as the dimensions are the same, the stress calculation should also be the same. The moral of this story is that both fibre stress and deflection need to be evaluated against different scenarios to ensure the software's basic model is performing correctly. The deflection part is particularly important (as seen in later tests) as it is the shared deflection of the pole and attached guys that determine how the applied loads are shared between them. Excessive pole deflection will make the guys carry more load and insufficient pole deflection will make the pole carry more load.
Here are the Test Results from Quick Pole and the required comparison with another leading software tool:
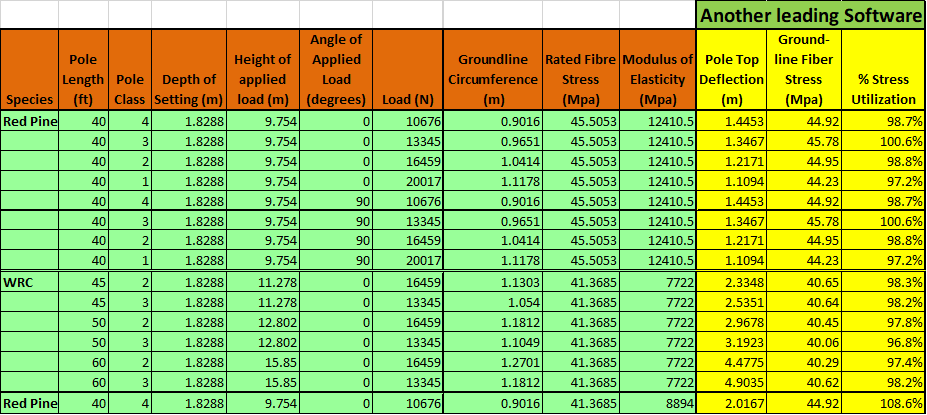
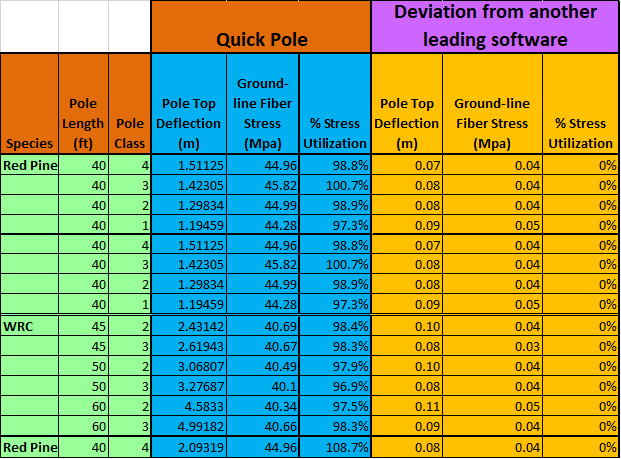
To demonstrate the results of our tests against Quick Pole, download the project files for ANSI and CSA based tests.
Guyed Structure Response
The focus of these tests are to ensure that the combined models of both the pole and the guying components work together in a consistent way to provide an accurate overall response. Individually the models may behave as expected, but when combined additional consistency constraints are demanded in order for them to work together properly.
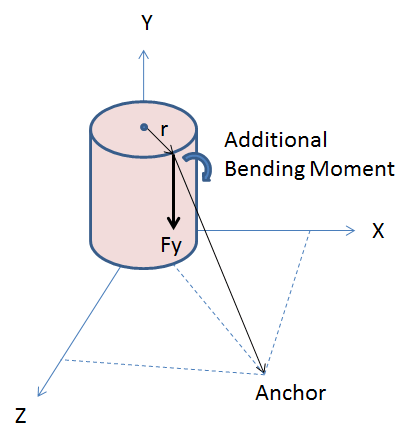 The amount that the pole or the guying components are permitted to deflect for a given amount of load is a critical determining factor for how much load each will carry. With respect to the law of diminishing returns, thicker poles or thicker guy wires will generally attract higher loads due to the fact that they are more "stiff" and have more resistance to deflection and stretch. This is the reason that the entire structure (poles plus guying components) must be solved as one unit and not independently.
The amount that the pole or the guying components are permitted to deflect for a given amount of load is a critical determining factor for how much load each will carry. With respect to the law of diminishing returns, thicker poles or thicker guy wires will generally attract higher loads due to the fact that they are more "stiff" and have more resistance to deflection and stretch. This is the reason that the entire structure (poles plus guying components) must be solved as one unit and not independently.
Another important aspect to consider is that all guying must be applied to the SIDE of the pole. It is not possible to actually or effectively guy at the very center of the pole. The vertical load applied to the side of the pole from guying creates bending moments, which are additional loads which must be considered. When more than one guying component is attached to the pole in the same direction, these guy-created bending moments can affect the sharing of the loads between them.
To fairly evaluate any software tool, the main aspect to consider in the testing is whether the loads are accurately shared between the pole and the guying. This includes along the length of the pole and moments in addition to just forces. While the specific tests should evaluate different heights of both load and guying attachments, multiple guying scenarios should also be included.
Model Tests
The focus of this category of tests is to confirm that the basic pole model with the addition of guying elements behaves as expected. It is important to validate that the pole and the guys share the loads in ways that are consistent with an established baseline. The model should not produce different results when loads and guys are placed at different angles. The use of strong and weak poles with guys attached close and far away from the loads, plus multiple guy scenarios, is the focus of these tests. To simulate stronger poles, tests are performed at lower levels of the pole where the pole is thicker.
The following tests are suggested:
- Use a 40 ft class 4 pole. Species to be Red Pine. Use NESC derived pole dimensions and Modulus of Elasticity.
- Apply a 10000N load at 2 feet from the top of the pole (9.75m).
- Place a 3/8" Grade 160 (or HS grade) guy wire at the load point to an anchor with a lead of 4 meters
- Measure deflection, forces, moments and fiber stresses at the guy location.
- Repeat the above test similating an overhead span guy of 40 meters with no effective vertical elevation changes.
- Repeat the above tests with the guy attachment lowered to 5 meters
- Repeat the above test with the load and guy attachment points reversed.
- Repeat the above test with the load and guy attachment points both at 5 meters high.
- Repeat all above tests with an additional same guy attachment at 7.0 meters high.
- Repeat steps 1 to 6 with the load and guying rotated by 90 degrees to prove that the models are directionally insensitive.
- No wind or storm loads
- This is a Linear Analysis with loads applied without additional load factors applied. If non-factored loads are not possible when comparing another tool, divide the proposed load by the load factor before it is applied to the pole.
Guyed Model Tests
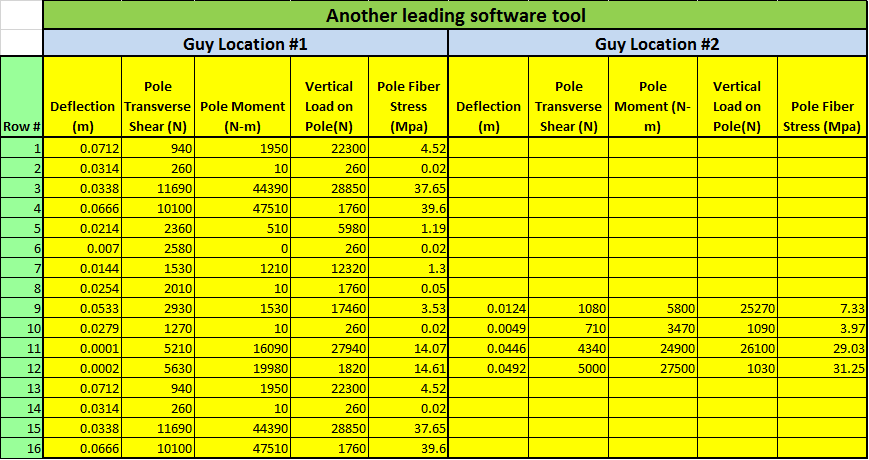
When compared to another software tool, Quick Pole compares as follows:
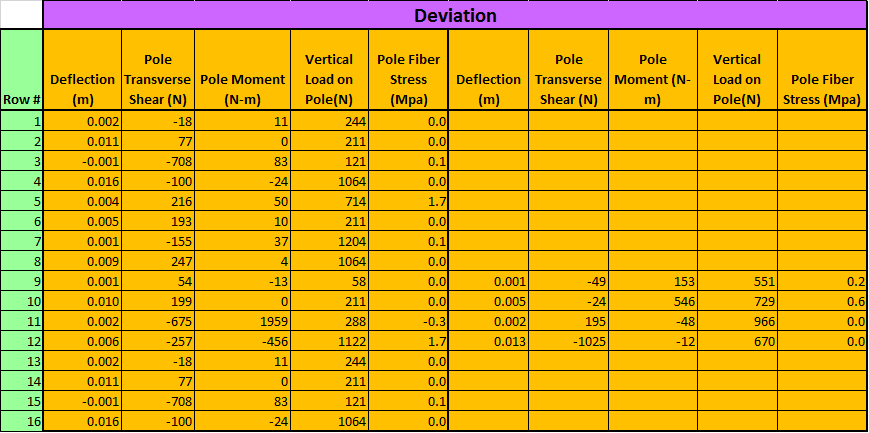
These are the results of our tests against Quick Pole. You can also use these Quick Pole Project Files to duplicate these results for yourself. For exact results, please ensure that the Line Grade is set to "No Overload Factors" so that the applied and static loads are not amplified.
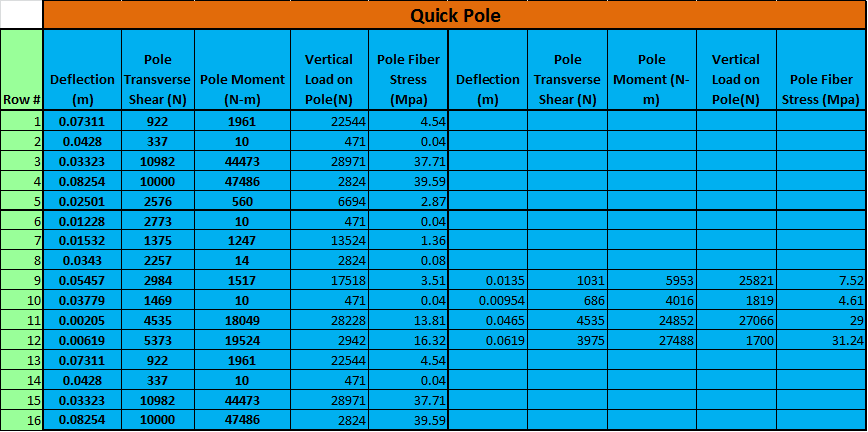
As a further test to validate that Quick Pole's model gives the same results with loads placed at different angles, the first and last four tests are compared directly:
Nonlinear
The focus of these tests are to ensure that Nonlinearities that are important to the structural analysis of poles and pole lines are thoroughly addressed. How well are the Nonlinear Analysis methodologies applied:
- Nonlinearity of member reactions due to structure deflection (Geometric Nonlinearity)
- Nonlinearity of loads due to structure deflection (Attachment Load Nonlinearity).
Geometric Nonlinearity
This Nonlinear methodology is the one most often referred to in Codes. It was developed initially to better assess poles with heavy equipment. However, it was found that all structures are better assessed when this Nonlinear analysis method is used. The tests are broken down into structures without guying first, followed by those that include guying. Without guying, this Nonlinearity is essentially the familiar P-Delta effect. For Geometric Nonlinearity with guys attached to the structures, the change in angle and length of any attached guying is also considered as the pole deflects.
The following structure tests are suggested. The loads were carefully chosen to be much less than the buckling capacity of the poles so that geometric effects are measured and not the software's ability to deal with "near-unstable" conditions.
- Use 40 ft, 50 ft and 60 ft poles; classes 4 and 1. Pole Species to be Red Pine with CSA rating for Modulus of Elasticity (8894 MPa).
- Apply a 20,000N vertical load at 2 feet from the top of the pole for the 40 ft pole, 15,000N for the 50 ft pole and 10,000N for the 60 ft pole. Also place a 1000 Newton horizontal load to help start the reaction.
- Perform a P-Delta Nonlinear analysis and note the pole top deflection and the Groundline stresses and moments.
- Repeat these tests using NESC ratings for Modulus of Elasticity and physical dimensions.
- On the 40 ft class 4 pole, add one guy at the vertical load attachment height that is at 90 degrees to the horizontal load at a lead of 5.0 meters.
- Note the guy component forces and the Groundline stresses and moments.
- No wind or storm loads.
- No overload factors.
The first set of tests (1-4) are used to validate the P-Delta like scenarios for both CSA and NESC rated poles.
The second set are to validate that the software tool does Guying Nonlinearity, which is required to be able to say that the tool performs a full Geometric Nonlinear Analysis. If the tool does not implement this feature, it will only support loads in its original direction plus generate vertical loads.
Both P-Delta and Guying Nonlinearity combined are required to prove the software tool implements a full Geometric Nonlinear Analysis.
P-Delta Model Tests
The following are the results of our tests against another software tool:
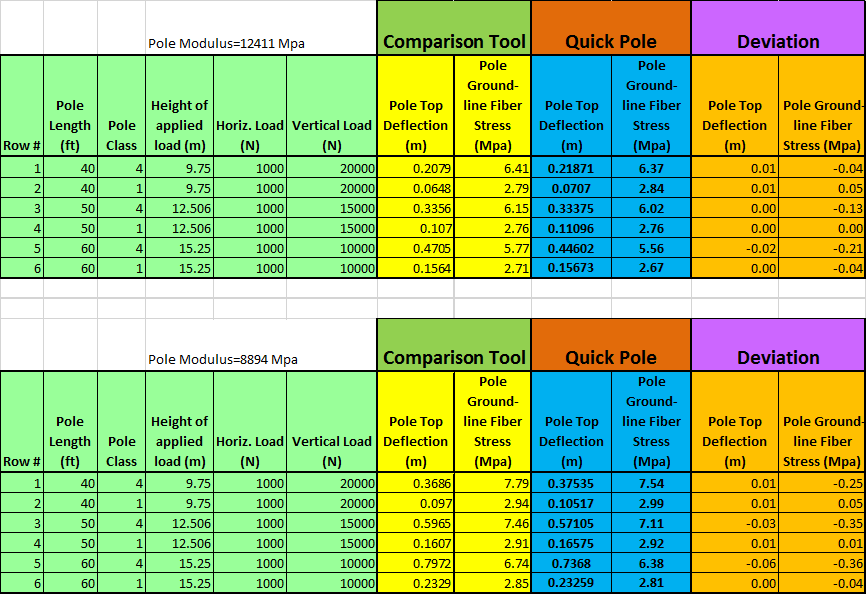
The results for NESC rated poles have the higher Modulus of Elasticity values. Both sets of results track very good. Especially when you note that almost all real pole structures will have some form of support which will limit the range of pole deflection possible. Download the Quick Pole project files you can use to help validate these results yourself.
Guying Nonlinearity Model Tests
The following are our tests of Quick Pole:
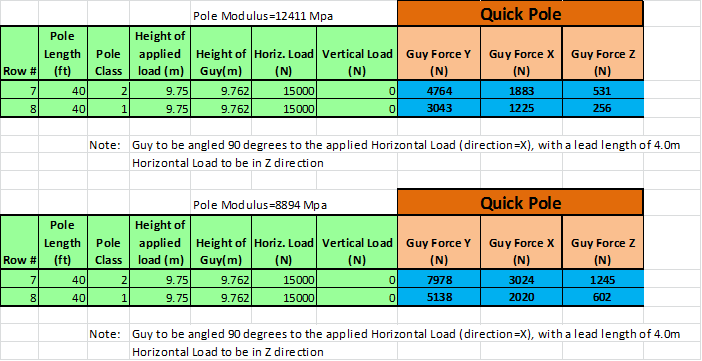
Download the Quick Pole project files you can use to help validate these results yourself.
These results show a couple specific key points:
- The stronger class of pole handles more of the load itself (stiffer poles deflect less).
- While the actual load was applied in the X direction and the guy/anchor was oriented in the Z direction (90 degrees out of line), the guy is able to take some of the load because it's model is updated to be not exactly in the Z direction as the pole deflects. If Quick Pole did not implement guying Nonlinearity, the guy loads shown above would have been zero.
Attachment Load Nonlinearity
This Nonlinear method captures the changes in the magnitude and angle of the applied loads as the pole deflects. In accordance with popular codes, all other poles are assumed to remain stationary. There are two main scenarios where this additional methodology greatly helps to model the structures more accurately:
- The balancing of inline tensions. Very common in scenarios where the span length on one side of the pole is much different than the other.
- The recognition that wire attachments can also handle some loads that the pole does not need to address all by itself. A common scenario is where two relatively balanced lines attached to a pole cross each other at 90 degrees and the wires can be shown to help support the lateral wind load.
This is an improvement over just doing a Geometric Nonlinear analysis as it more completely models how the pole would actually behave with the attached wires. If a software tool cannot address Attachment Load Nonlinearity, they should note this in their compliance matrix.
The following tests are suggested to assess the Inline Tension situation:
- Use 40 foot class 4 and 1 poles
- Attach one medium size wire at two feet from the top of the pole.
- Assume the span lengths are 40 meters and 60 meters.
- Calculate the final tensions of the wires on both sides of the pole, plus the pole top deflection and Groundline stresses.
- No storm loads
The following tests are suggested to assess the Wire Attachments carrying load situation:
- Use 40 ft class 4 and 1 poles
- Attach one medium size wire at two feet from the top of the pole with an average span length of 60 meters.
- Place another wire attachment at the same height and crossing the previous at 90 degrees.
- Apply horizontal load in the direction of the crossed wire with a magnitude of 3000 Newtons to simulate wind load.
- Calculate the final tensions of the wires in all directions, plus the pole top deflections.
- ½" ice and -20C storm loads, no wind
Model Tests
The loads that can change in response to the movement of the pole are the attachments that span to other poles. Wire attachments will have a starting maximum tension that would be applied to the poles. If the poles move towards each other, this lessens the tension. Conversely, poles that try to move apart result in an increase in wire tensions. The wires will behave this way regardless of what situation is causing the effect. In practice, two main situations arise:
- Balancing of un-equal inline tensions. Some software tools use an average span length for both sides of the pole before calculating their tensions. Quick Pole calculates tensions based on actual span lengths and then shows the end result of the pole deflecting/stressing and the wire tensions changing.
- Support of wind load applied to a pole by wire attachments going to poles in lateral directions. This is a minor impact and is more of a Geometric Nonlinearity related to the attachment loads. Since the span lengths are long compared to the pole's deflection, the angles created are small and therefore the impacts are small. These results can be seen in the Attachment Load Changes report.
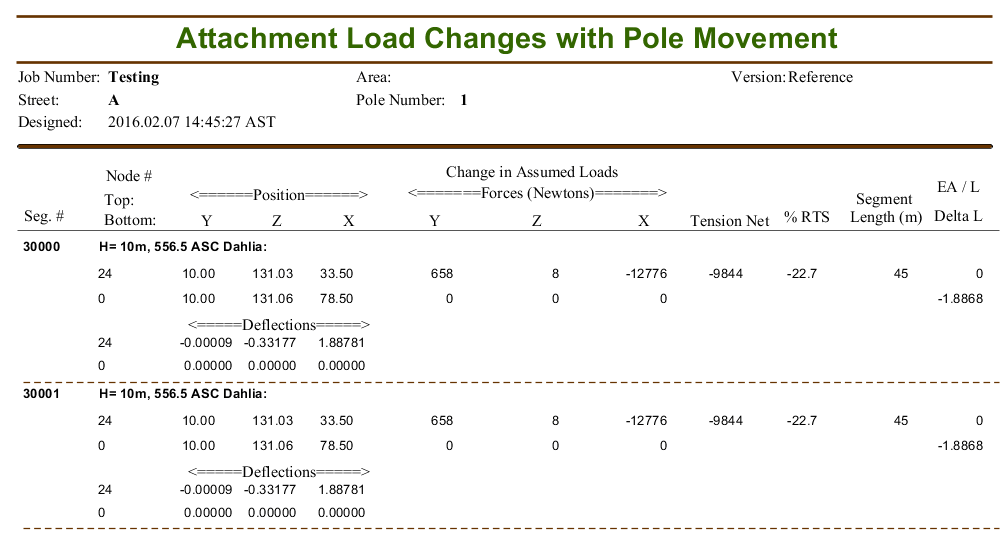
Download a project file showing an extreme example of this effect. It has five 556.5 ASC Dahlia conductors attached in one direction from an unsupported 40 ft Class 4 WRC cedar pole. Under CSA Heavy Loading, the maximum tension applied to the pole by each of the wires is 10990 Newtons, or 25% RTS. Under this load from all five wires, the pole's tip deflects about 1.89 meters, which in turn reduces the tension in these wires to about 3% RTS. Again, this is an extreme example that is not typical; but sufficient to demonstrate the ability of Quick Pole to re-calculate wire tensions during the analysis procedure as the pole deflects.
Foundation
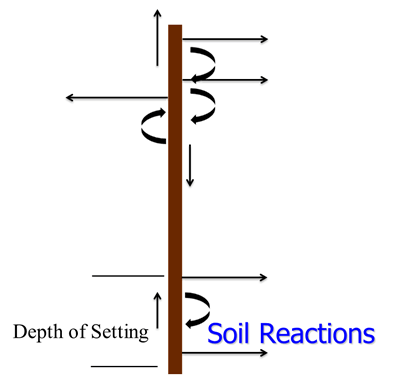 Both the CSA and NESC (and likely others) state that the foundation of the pole must be able to withstand the loads transferred to it by the pole. Neither provide much guidance however as to how to evaluate this requirement. To that end we offer some discussion.
Both the CSA and NESC (and likely others) state that the foundation of the pole must be able to withstand the loads transferred to it by the pole. Neither provide much guidance however as to how to evaluate this requirement. To that end we offer some discussion.
The pole experiences various vertical loads plus lateral forces and moments from possibly any direction. The Soil Foundation is an important part of the restraining mechanism for the structure. Without it, the pole would simply fall over.
From a modeling perspective, almost all Pole Line Design software tools evaluate the pole structure without regard to its foundation. For those software tools that do consider the foundation's ability to support the pole, the required Soil Reactions are usually calculated assuming that the Soil Foundation is very rigid.
Soil Reactions
The following are the major reactions that should be evaluated as part of the Foundation strength requirement:
- Vertical Load Capacity: The soil directly beneathe the pole's butt must not fail under Vertical Load.
- Lateral Load Capacity: The soil must hold the pole vertical while it is holding the required amount of lateral forces and moments at the groundline.
- Uplift Capacity: In cases when the pole is subjected to a net upwards vertical force, the soil's ability to restrain the pole must be evaluated.
Each reaction test will be discussed separately so as to describe how these calculations can be performed.
Vertical Load Capacity
Poles can be subjected to large vertical loads under heavy guying conditions. This net vertical force onto the pole can be significant enough to cause the soil to fail. By failure we mean that the soil failed to restrict the pole from moving under the required load. The common definition of soil failure is when the soil "gives" more than 1 inch (25mm).
There are several methodologies and theories available to evaluate this requirement. Most come from evaluation of shallow footings.
Lateral Load Capacity
Particularly for Unguyed poles but for others as well, there can be significant groundline moments and forces required for the soil to support. Since soil as a material has certain properties such as cohesion, shear strength, friction, it is reasonable to expect that strong groundline moments may required deeper setting depths or stronger soil.
Here are the most common approaches to evaluating lateral soil capacity, in order of increasing accuracy:
- Is Depth of Setting equal to or better than 10% of the pole's length plus two feet (0.61m)?
- RUS Bulletin 1724E-200, chapter 12. Tests categorize soils as good, average and poor.
- Effective Stress Analysis methods such as those proposed by Broms and Flemming. Uses soil parameters such as soil friction angle and undrained shear strength.
- P - Y curves approach corelating pole deflections to corresponding soil reactions at all depths.
- Finite Element Analysis techniques.
Uplift Capacity
Anyone that has ever seen the stub of a pole being pulled out of the ground by a truck with a boom winch, knows that the truck is going to need to work hard in order to pull it out of the ground. Oftentimes the ground next to the pole stub is loosened first in order to make it possible in the first place.
There are two well know mechanisms that help keep a pole from being lifted out of the ground:
- Skin Resistance: The friction of the soil against the side of the pole below ground level.
- Anchoring Effect: Since most poles are tapered, the difference between the pole's butt diameter and that at groundline serves to help anchor the pole in the ground.
Both of these effects increase along the depth of the pole and vary with soil properties and the depth of the water table.
For poles with a Push Brace attached, it is very possible that the pole's weight and that of its attachments may not be enough to overcome the Push Brace's upward force that is generates. Another scenario of vertical uplift can occur when a pole line's elevation changes quickly, possibly combined with low temperatures. In both cases it is important to understand if the pole will stay in the ground or pull out and fall over.
Model Tests
There are few Pole Line Design software tools in existence that consider all of the above aspects of Foundation strength. It is therefore proposed that it is most appropriate to ask software tools to clarify IF they do ANY of these calculations, and if they do, what technique is used.
Coupled with this, if any tests are performed, what Soil parameters are used and what Safety Factors are applied to the results.
Here are the answers w.r.t Quick Pole:
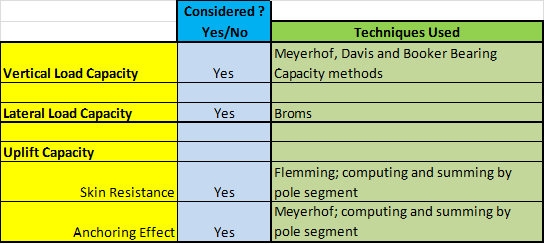
For comparison with others, below we openly share the Soil Parameters used with the methods shown above.
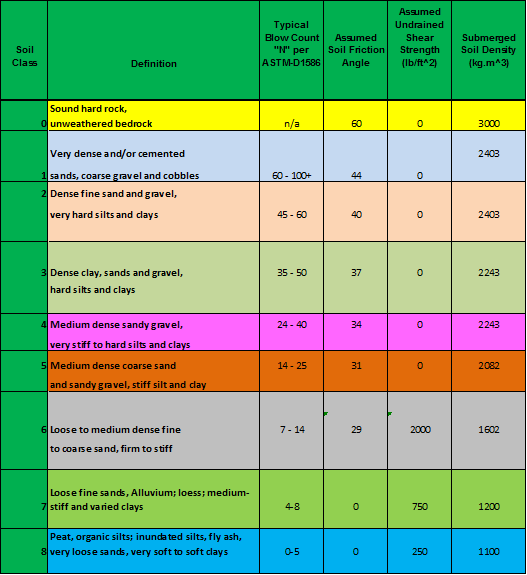
Example of Soil Failure from Lateral Loads around a pole
Street / Lead
Pole Stresses are only based on a Linear Analysis (not Nonlinear) based on Project Setting.
The Soil around the pole CANNOT support the Pole's Groundline Moments (104134 N-M) required.
Required Depth of Setting = 1.991 m. Current Depth of Setting = 1.829 m. Soil Class= 1
Worst Wind Direction for Pole Loading is 90°
The Vertical Load capacity of the Soil directly below the pole is within defined limits.
Capacity = 139 KN (1819 Kpa Bearing Capacity + 4 KN skin resistance. Soil Safety Factor= 1). Load = 9 KN
Example of Push brace being pulled out of the ground and the Soil Capacity trying to resist
Pole Stresses are only based on a Linear Analysis (not Nonlinear) based on Project Setting.
Soil Groundline Moment tests were not performed since the pole is guyed. Groundline Moments = 13937 N-M.
Worst Wind Direction for Pole Loading is 90°
The Vertical Load capacity of the Soil directly below the pole is within defined limits.
Capacity = 139 KN (1819 Kpa Bearing Capacity + 4 KN skin resistance. Soil Safety Factor= 1). Load = 45 KN
Push Brace is being pulled out of the ground !
Net Positive (upward) Force = -31.035 KN
Example of Push brace lifting the supported pole out of the ground and the Soil Capacity trying to resist
Street / Lead
Pole Stresses are only based on a Linear Analysis (not Nonlinear) based on Project Setting.
Soil Groundline Moment tests were not performed since the pole is guyed. Groundline Moments = 14413 N-M.
Worst Wind Direction for Pole Loading is 90°
Pole is being lifted out of the ground !
Pole and Attachment weights plus factored soil resistance of 5 KN is insufficient.
Net Positive (upward) Force = -11 KN
Push Brace Compression Forces of 32 KN requires a 35 ft Cl 5 pole. This class Push Brace has a Factored Compression Capacity of 181 KN.
The Vertical Load Capacity of the Soil directly below the Push Brace is within defined limits.